
分析 (1)求出f(x)的导数,并分解因式,对a讨论,分a≤0,a>2,0<a<2,求得单调区间,可得所求极值点;
(2)求出g(x)的解析式和导数,由题意可得2x2-(a+2)x+2=0有两个不为1的正根,运用判别式大于0和韦达定理,可得a>2,化简g(x1)•g(x2),由不等式的性质即可得证.
解答 解:(1)函数f(x)=$\frac{-{x}^{2}+ax-a}{{e}^{x}}$(x>0)的导数为f′(x)=$\frac{{x}^{2}-(a+2)x+2a}{{e}^{x}}$=$\frac{(x-a)(x-2)}{{e}^{x}}$,
当a≤0时,由x>0,则x-a>0,当x>2时,f′(x)>0,f(x)递增;
当0<x<2时,f′(x)<0,f(x)递减.
可得x=2为f(x)的极小值点;
当a>2时,由x>a或0<x<2时,f′(x)>0,f(x)递增;
当2<x<a时,f′(x)<0,f(x)递减.
可得x=2为f(x)的极大值点;x=a为f(x)的极小值点;
当0<a<2时,由x>2或0<x<a时,f′(x)>0,f(x)递增;
当a<x<2时,f′(x)<0,f(x)递减.
可得x=a为f(x)的极大值点;x=2为f(x)的极小值点.
综上可得,当a≤0时,f(x)的极小值点为x=2,无极大值点;
当a>2时,f(x)的极小值点为x=a,极大值点为x=2;
当0<a<2时,f(x)的极小值点为x=2,极大值点为x=a;
(2)证明:g(x)=$\frac{f(x)+f′(x)}{x-1}$
=$\frac{(-{x}^{2}+ax-a)+({x}^{2}-ax-2x+2a)}{{(x-1)•e}^{x}}$=$\frac{a-2x}{(x-1)•{e}^{x}}$,
g′(x)=$\frac{2{x}^{2}-(a+2)x+2}{(x-1)^{2}•{e}^{x}}$,
由函数g(x)在(0,1)∪(1,+∞)内有两个极值点x1,x2,
可得2x2-(a+2)x+2=0有两个不为1的正根,
即有△=(a+2)2-16>0,解得a>2或a<-6,
且x1+x2=$\frac{a+2}{2}$>0,x1x2=1,
解得a>2.
则g(x1)•g(x2)=$\frac{a-2{x}_{1}}{({x}_{1}-1)•{e}^{{x}_{1}}}$•$\frac{a-2{x}_{2}}{({x}_{2}-1)•{e}^{{x}_{2}}}$=$\frac{{a}^{2}-2a({x}_{1}+{x}_{2})+4{x}_{1}{x}_{2}}{({x}_{1}{x}_{2}+1-{x}_{1}-{x}_{2})•{e}^{{x}_{1}+{x}_{2}}}$=$\frac{4-2a}{\frac{2-a}{2}•{e}^{\frac{2+a}{2}}}$=$\frac{4}{{e}^{1+\frac{a}{2}}}$,
由a>2可得e${\;}^{1+\frac{a}{2}}$>e2,
即有$\frac{4}{{e}^{1+\frac{a}{2}}}$<$\frac{4}{{e}^{2}}$.
则g(x1)•g(x2)<$\frac{4}{{e}^{2}}$.
点评 本题考查导数的运用:求单调区间和极值,同时考查不等式的证明,注意运用韦达定理和判别式,考查分类讨论的思想方法,化简整理的运算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
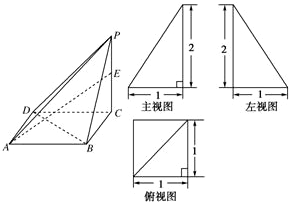 已知四棱锥P-ABCD的三视图如图所示,E是侧棱PC上的动点.
已知四棱锥P-ABCD的三视图如图所示,E是侧棱PC上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (1,+∞) | C. | [2,+∞) | D. | [1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com