
���� ��1����������ת�ƣ�����������̣���ȥ��������������C�����ͨ���̣�
��2����P��x��y����A��x0��y0������A������C���ϣ�D��0��2������A������C���ϣ��г������飬������AD�е�P�Ĺ켣���̣�
��� �⣺��1����$\left\{\begin{array}{l}{x=4cos��}\\{y=3sin��}\end{array}\right.$����Ϊ������������$\left\{\begin{array}{l}{{x}^{��}=\frac{1}{2}x}\\{{y}^{��}=\frac{1}{3}y}\end{array}\right.$���õ�����C��IJ�������$\left\{\begin{array}{l}{x��=2cos��}\\{y��=sin��}\end{array}\right.$��
������C�����ͨ���̷���Ϊ$\frac{{x}^{2}}{4}+{y}^{2}$=1��
��2����P��x��y����A��x0��y0������D��0��2������AD�е�ΪP
����$\left\{\begin{array}{l}{{x}_{0}=2x}\\{{y}_{0}=2y-2}\end{array}\right.$
�ֵ�A������C'�ϣ������C'����ͨ���̵�x2+��2y-2��2=1
�ද��P�Ĺ켣����Ϊx2+4��y-1��2=1�� ����10�֣�
���� ���⿼��������̺�ֱ������Ļ���������ֱ�����귽����������̼�Ĺ�ϵ��������뷨�����ã��������������


 ����ʦ���һ��һ��ϵ�д�
����ʦ���һ��һ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 29-37 | B�� | 210-46 | C�� | 211-56 | D�� | 212-67 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
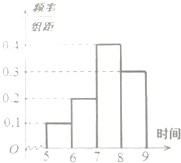 ijУ�����꼶����2000��ѧ��������������1200�ˣ�Ů����800�ˣ�Ϊ���˽��꼶ѧ����˯��ʱ���������ְ��շֲ�����ķ������г�ȡ��100��ѧ����˯��ʱ����������ݣ����������ͼ��Ƶ�ʷֲ�ֱ��ͼ��
ijУ�����꼶����2000��ѧ��������������1200�ˣ�Ů����800�ˣ�Ϊ���˽��꼶ѧ����˯��ʱ���������ְ��շֲ�����ķ������г�ȡ��100��ѧ����˯��ʱ����������ݣ����������ͼ��Ƶ�ʷֲ�ֱ��ͼ��| �Ա�ʱ�� | ���� | Ů�� |
| ˯��ʱ������7Сʱ | ||
| ˯��ʱ�䲻����7Сʱ |
| P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��1�� | B�� | ��2��2�� | C�� | ��3��3�� | D�� | ��4��4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��l1��l2��l3��ͬһƽ���ڵ�����ƽ��ֱ�ߣ�l2��l3��l1��ͬ�࣮l1��l2�ľ�����d��l2��l3�ľ�����2d���߳�Ϊ1����������ABC����������ֱ���l1��l2��l3�ϣ���d=$\frac{{\sqrt{21}}}{14}$��
��ͼ��l1��l2��l3��ͬһƽ���ڵ�����ƽ��ֱ�ߣ�l2��l3��l1��ͬ�࣮l1��l2�ľ�����d��l2��l3�ľ�����2d���߳�Ϊ1����������ABC����������ֱ���l1��l2��l3�ϣ���d=$\frac{{\sqrt{21}}}{14}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 6 | C�� | 9 | D�� | 4$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 16$\sqrt{2}$ | B�� | 8$\sqrt{2}$ | C�� | 8$\root{3}{4}$ | D�� | 4$\root{3}{4}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com