
| A. | 29-37 | B. | 210-46 | C. | 211-56 | D. | 212-67 |
分析 先设每个30分钟进去的人数构成数列{an},利用观察法求数列{an}的通项公式,求数列{an}的前11项和,由等比数列前n项和公式即可得上午11时公园内的人数.
解答 解:设每个30分钟进去的人数构成数列{an},
则a1=1=1-0,
a2=2-1,
a3=4-2,
a4=8-3,
a5=16-4
…
an=2n-1-(n-1)
设数列{an}的前n项和为Sn
依题意,到上午11点公园内的人数是此数列的前11项的和,
所以s11=(1-0)+(2-1)+(22-2)+(23-3)+…+(210-10)
=(1+2+22+23+…+210)-(1+2+…+10)
=$\frac{1-{2}^{11}}{1-2}$-$\frac{10(1+10)}{2}$=211-56.
故选:C.
点评 本题考察了观察法求数列的通项公式,归纳推理出数列的通项公式以及求等差数列、等比数列的前n项和公式,解题时要善于将实际问题转化为数学问题,运用数学知识解决问题,还要具有较强的观察能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2n+3 | B. | 2n+1 | C. | 3n+2 | D. | 4n+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2] | B. | (-∞,-2) | C. | (-∞,-6] | D. | (-∞,-6) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
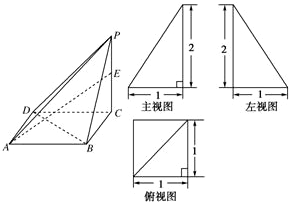 已知四棱锥P-ABCD的三视图如图所示,E是侧棱PC上的动点.
已知四棱锥P-ABCD的三视图如图所示,E是侧棱PC上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com