
| A. | (-∞,-2] | B. | (-∞,-2) | C. | (-∞,-6] | D. | (-∞,-6) |
分析 由题意可得a≤$\frac{1}{x}$-$\frac{3}{{x}^{3}}$-$\frac{4}{{x}^{2}}$在x∈[-4,-1]∪[1,4]的最小值,由f(x)=$\frac{1}{x}$-$\frac{3}{{x}^{3}}$-$\frac{4}{{x}^{2}}$,求得导数,判断单调性可得最小值,可得a的范围.
解答 解:当x∈[-4,-1]∪[1,4]时,不等式ax2-x+4+$\frac{3}{x}$≤0恒成立,
即为a≤$\frac{1}{x}$-$\frac{3}{{x}^{3}}$-$\frac{4}{{x}^{2}}$在x∈[-4,-1]∪[1,4]的最小值,
由f(x)=$\frac{1}{x}$-$\frac{3}{{x}^{3}}$-$\frac{4}{{x}^{2}}$的导数为f′(x)=-$\frac{1}{{x}^{2}}$+$\frac{9}{{x}^{4}}$+$\frac{8}{{x}^{3}}$=$\frac{9+8x-{x}^{2}}{{x}^{4}}$,
由x∈[1,4]可得9+8x-x2>0,即有区间[1,4]为增区间,
即有f(1)为[1,4]上的最小值,且为-6;
由x∈[-4,-1]可得9+8x-x2≤0,即有区间[-4,-1]为减区间,
即有f(-1)为[-4,-1]上的最小值,且为-2.
可得f(x)在x∈[-4,-1]∪[1,4]的最小值为-6.
即有a≤-6.
故选:C.
点评 本题考查不等式恒成立问题的解法,注意运用参数分离和构造函数,运用导数判断单调性求得最值,考查化简整理的运算能力,属于中档题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 29-37 | B. | 210-46 | C. | 211-56 | D. | 212-67 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数值域为[1,π] | B. | 此函数不单调 | C. | 此函数为偶函数 | D. | 方程f[f(x)]=x有两解 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
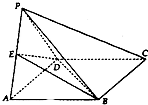 如图,△PAD与正方形ABCD共用一边AD,平面PAD⊥平面ABCD,其中PA=PD,AB=2,点E是棱PA的中点.
如图,△PAD与正方形ABCD共用一边AD,平面PAD⊥平面ABCD,其中PA=PD,AB=2,点E是棱PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,l1,l2,l3是同一平面内的三条平行直线,l2,l3在l1的同侧.l1与l2的距离是d,l2与l3的距离是2d,边长为1的正三角形ABC的三个顶点分别在l1,l2,l3上,则d=$\frac{{\sqrt{21}}}{14}$.
如图,l1,l2,l3是同一平面内的三条平行直线,l2,l3在l1的同侧.l1与l2的距离是d,l2与l3的距离是2d,边长为1的正三角形ABC的三个顶点分别在l1,l2,l3上,则d=$\frac{{\sqrt{21}}}{14}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com