
分析 根据题意画出图形,结合图形利用正弦定理,求出当∠OPA取最大值时∠A的值,从而求出PA的值.
解答 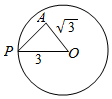 解:如图所示,
解:如图所示,
△OPA中,OP=3,OA=$\sqrt{3}$,
由正弦定理得,$\frac{OA}{sin∠OPA}$=$\frac{OP}{sin∠A}$,
所以sin∠OPA=$\frac{OA•sin∠A}{OP}$=$\frac{\sqrt{3}•sin∠A}{3}$;
又OP>OA,
所以当∠OPA取最大值时,sin∠A=1,
即∠A=90°,
所以PA=$\sqrt{{OP}^{2}{-OA}^{2}}$=$\sqrt{{3}^{2}{-(\sqrt{3})}^{2}}$=$\sqrt{6}$.
故答案为:$\sqrt{6}$.
点评 本题考查了正弦定理与勾股定理的应用问题,是基础题目.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
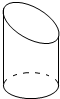 如图,一个底面半径为R的圆柱被与底面成30°二面角的平面所截,截面是一个椭圆,则该椭圆的焦距是( )
如图,一个底面半径为R的圆柱被与底面成30°二面角的平面所截,截面是一个椭圆,则该椭圆的焦距是( )| A. | R | B. | 2R | C. | $\frac{{\sqrt{3}}}{3}$R | D. | $\frac{{2\sqrt{3}}}{3}$R |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 29-37 | B. | 210-46 | C. | 211-56 | D. | 212-67 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
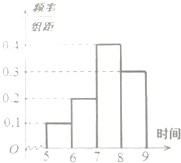 某校高三年级共有2000名学生,其中男生有1200人,女生有800人.为了了解年级学生的睡眠时间的情况,现按照分层抽样的方法从中抽取了100名学生的睡眠时间的样本数据,并绘成了如图的频率分布直方图.
某校高三年级共有2000名学生,其中男生有1200人,女生有800人.为了了解年级学生的睡眠时间的情况,现按照分层抽样的方法从中抽取了100名学生的睡眠时间的样本数据,并绘成了如图的频率分布直方图.| 性别时间 | 男生 | 女生 |
| 睡眠时间少于7小时 | ||
| 睡眠时间不少于7小时 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com