
| A. | (-1,1) | B. | (1,+∞) | C. | [2,+∞) | D. | [1,2) |
分析 由f(0)=ln1=0,可得:x=0是函数y=f(x)-kx的一个零点;当x<0时,由f(x)=kx,得-x2+$\frac{1}{2}$x=kx,解得x=$\frac{1}{2}$-k,由x=$\frac{1}{2}$-k<0,可得:k>$\frac{1}{2}$;当x>0时,函数f(x)=ex-1,由f'(x)∈(1,+∞),进而可得k>1;综合讨论结果,可得答案.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}-{x^2}+\frac{1}{2}x,x<0\\{e^x}-1,x≥0\end{array}$,
∴f(0)=ln1=0,
∴x=0是函数y=f(x)-kx的一个零点,
当x<0时,由f(x)=kx,
得-x2+$\frac{1}{2}$x=kx,
即-x+$\frac{1}{2}$=k,解得x=$\frac{1}{2}$-k,
由x=$\frac{1}{2}$-k<0,解得k>$\frac{1}{2}$,
当x>0时,函数f(x)=ex-1,
f'(x)=ex∈(1,+∞),
∴要使函数y=f(x)-kx在x>0时有一个零点,
则k>1,
∴k>1,
即实数k的取值范围是(1,+∞),
故选:B.
点评 本题考查的知识点是函数零点及零点的个数,二次函数的图象和性质,指数型函数的图象和性质,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
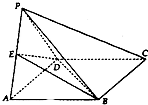 如图,△PAD与正方形ABCD共用一边AD,平面PAD⊥平面ABCD,其中PA=PD,AB=2,点E是棱PA的中点.
如图,△PAD与正方形ABCD共用一边AD,平面PAD⊥平面ABCD,其中PA=PD,AB=2,点E是棱PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
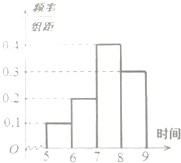 某校高三年级共有2000名学生,其中男生有1200人,女生有800人.为了了解年级学生的睡眠时间的情况,现按照分层抽样的方法从中抽取了100名学生的睡眠时间的样本数据,并绘成了如图的频率分布直方图.
某校高三年级共有2000名学生,其中男生有1200人,女生有800人.为了了解年级学生的睡眠时间的情况,现按照分层抽样的方法从中抽取了100名学生的睡眠时间的样本数据,并绘成了如图的频率分布直方图.| 性别时间 | 男生 | 女生 |
| 睡眠时间少于7小时 | ||
| 睡眠时间不少于7小时 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,l1,l2,l3是同一平面内的三条平行直线,l2,l3在l1的同侧.l1与l2的距离是d,l2与l3的距离是2d,边长为1的正三角形ABC的三个顶点分别在l1,l2,l3上,则d=$\frac{{\sqrt{21}}}{14}$.
如图,l1,l2,l3是同一平面内的三条平行直线,l2,l3在l1的同侧.l1与l2的距离是d,l2与l3的距离是2d,边长为1的正三角形ABC的三个顶点分别在l1,l2,l3上,则d=$\frac{{\sqrt{21}}}{14}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com