
分析 (Ⅰ)相关点代入法求轨迹方程.(Ⅱ)直线与方程联立,求出交点的横坐标,表示出三角形的面积并通过函数求出最值.
解答 解:(Ⅰ)设Q(x0,y0),P(x,y)则M(x0,0),$\overrightarrow{MP}=(x-{x}_{0,}y)$,$\overrightarrow{MQ}=(0,{y}_{0})$
由$\overrightarrow{MP}=\sqrt{2}\overrightarrow{MQ}$,得$\left\{\begin{array}{l}{x-{x}_{0}=0}\\{y=\sqrt{2}{y}_{0}}\end{array}\right.$⇒$\left\{\begin{array}{l}{{x}_{0}=x}\\{{y}_{0}=\frac{\sqrt{2}}{2}y}\end{array}\right.$
代入圆的方程中,得P点的轨迹方程:${x^2}+\frac{y^2}{2}=1$
所以曲线Γ是焦点在y轴上的椭圆,焦点坐标分别为(0,1)与(0,-1)…(4分)
当AB的斜率存在时,设AB的方程为:y=kx与Γ的方程联立,
消去y,整理得$x=±\frac{{\sqrt{2}}}{{\sqrt{{k^2}+2}}}$,设A(x1,y1),B(x2,y2)
则$|{{x_1}-{x_2}}|=\frac{{2\sqrt{2}}}{{\sqrt{{k^2}+2}}},|{{y_1}-{y_2}}|=\frac{{2\sqrt{2}|k|}}{{\sqrt{{k^2}+2}}}$|AB|=$\sqrt{({x}_{1}{-{x}_{2})}^{2}+({y}_{1}{-{y}_{2})}^{2}}$=$\frac{\sqrt{8({k}^{2}+1)}}{\sqrt{{k}^{2}+2}}$,…(8分)
设$C(0,\frac{{\sqrt{2}k}}{{\sqrt{{k^2}+2}}})$,则点C到直线AB的距离$d=\frac{{\sqrt{2}|k|}}{{\sqrt{({k^2}+1)({k^2}+2)}}}$,${S}_{△ABC}=\frac{1}{2}|AB|d=\frac{2|k|}{{k}^{2}+2}$…(10分)
当k=0时,S=0,当k≠0时$S=\frac{2}{{|k|+\frac{2}{|k|}}}≤\frac{{\sqrt{2}}}{2}$,当$k=±\sqrt{2}$时取等号
故三角形ABC面积的最大值为$\frac{{\sqrt{2}}}{2}$…(12分)
点评 本题主要考查(Ⅰ)相关点代入法求轨迹方程.(Ⅱ)直线与方程联立,求出交点的横坐标,表示出三角形的面积并通过函数求出最值


科目:高中数学 来源: 题型:解答题
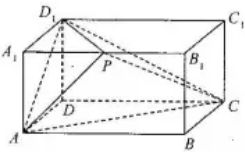 长方体ABCD-A1B1C1D1中,AB=2AD=2AA1=2,P为A1B1中点.
长方体ABCD-A1B1C1D1中,AB=2AD=2AA1=2,P为A1B1中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知C为AB为直径的圆O上任意一点,且△SAC为等边三角形,平面SAC⊥平面ABC.
已知C为AB为直径的圆O上任意一点,且△SAC为等边三角形,平面SAC⊥平面ABC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com