
分析 (1)利用绝对值三角不等式求得f(x)的最小值,再根据f(x)的最小值为2,求得a的值.
(2)由题意可得,x∈[-2,-1]时,f(x)≤|2x-4|恒成立,即-5+a≤2x≤5+a恒成立,即$\left\{\begin{array}{l}{-5+a≤-4}\\{-2≤5+a}\end{array}\right.$,由此求得a的范围.
解答 解:(1)∵函数f(x)=|2x+1|+|2x-a|≥|2x+1-(2x-a)|=|a+1|,且f(x)的最小值为2,
∴|a+1|=2,∴a=1 或a=-3.
(2)f(x)≤|2x-4|的解集包含[-2,-1],即x∈[-2,-1]时,f(x)≤|2x-4|恒成立,
即|2x+1|+|2x-a|≤|2x-4|恒成立,即-2x-1+|2x-a|≤4-2x恒成立,
即|2x-a|≤5恒成立,即-5+a≤2x≤5+a恒成立,即$\left\{\begin{array}{l}{-5+a≤-4}\\{-2≤5+a}\end{array}\right.$,∴-7≤a≤1.
点评 本题主要考查绝对值三角不等式的应用,绝对值不等式的解法,函数的恒成立问题,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{3}{2}$] | B. | (0,$\frac{9}{4}$] | C. | (0,3] | D. | (0,9] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16$\sqrt{2}$ | B. | 8$\sqrt{2}$ | C. | 8$\root{3}{4}$ | D. | 4$\root{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
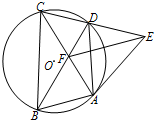 如图,四边形ABCD内接于圆O,AC与BD相交于点F,AE与圆O相切于点A,与CD的延长线相交于点E,∠ADE=∠BDC.
如图,四边形ABCD内接于圆O,AC与BD相交于点F,AE与圆O相切于点A,与CD的延长线相交于点E,∠ADE=∠BDC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{37}$-1 | B. | $\frac{8\sqrt{5}}{5}$ | C. | $\frac{8\sqrt{5}-5}{5}$ | D. | $\sqrt{37}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com