
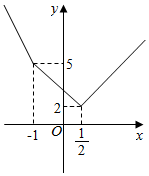 已知函数f(x)=|2x-1|+|x-a|,g(x)=x-1.
已知函数f(x)=|2x-1|+|x-a|,g(x)=x-1.分析 (1)当a=-1时,不等式f(x)>g(x)化为|2x-1|+|x+1|-x+1>0,去掉绝对值,作出函数的图象,即可求不等式f(x)<g(x)的解集.
(2)如果?x∈R,f(x)≥1恒成立,只需f(x)的最小值大于等于1即可.
解答 解:(1)当a=-1时,不等式f(x)>g(x)化为|2x-1|+|x+1|-x+1>0,
设函数$y=\left\{\begin{array}{l}-4x+1,x<-1\\-2x+3,-1≤x≤\frac{1}{2}\\ 2x+1,x>\frac{1}{2}\end{array}\right.$
其图象如图所示,从图象可知,当且仅当x∈R时,y>0,
所以原不等式的解集为{x|x∈R}
(2)?x∈R,f(x)≥1恒成立,只需f(x)的最小值大于等于1即可,
当$a≥\frac{1}{2}$时,$f(x)=|{2x-1}|+|{x-a}|=\left\{\begin{array}{l}-3x+a+1,x<\frac{1}{2}\\ x+a-1,\frac{1}{2}≤x≤a\\ 3x-a-1,x>a\end{array}\right.$,∴$f{(x)_{min}}=a-\frac{1}{2}$
同理,当$a<\frac{1}{2}$时,$f{(x)_{min}}=\frac{1}{2}-a$
∴$\left\{\begin{array}{l}a≥\frac{1}{2}\\ a-\frac{1}{2}≥1\end{array}\right.$或$\left\{\begin{array}{l}a<\frac{1}{2}\\ \frac{1}{2}-a≥1\end{array}\right.$,解得$a≥\frac{3}{2}$或$a≤\frac{1}{2}$
∴a的取值范围是$({-∞,-\frac{1}{2}}]∪[{\frac{3}{2},+∞})$.
点评 本题考查绝对值不等式的解法,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$<$\frac{1}{2n-1}$ (n≥2) | B. | 1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$<<$\frac{2n+1}{n}$ (n≥2) | ||
| C. | 1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$<$\frac{2n-1}{n}$ (n≥2) | D. | 1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$<<$\frac{2n}{2n+1}$ (n≥2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
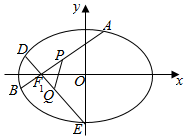 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,点M(1,$\frac{{\sqrt{2}}}{2}}$)在椭圆C上.
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,点M(1,$\frac{{\sqrt{2}}}{2}}$)在椭圆C上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>0 | B. | a>1 | C. | a>$\sqrt{2}$ | D. | a>2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\sqrt{2}$,$\sqrt{2}$] | B. | (-∞,-$\sqrt{2}$]∪[$\sqrt{2}$,+∞) | C. | (1,$\sqrt{2}$) | D. | [1,$\sqrt{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com