
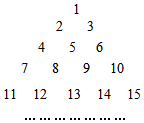 将全体正整数排成一个三角形数阵:按照以上排列的规律,第20行(n≥3)从左到右的第3个数为208.
将全体正整数排成一个三角形数阵:按照以上排列的规律,第20行(n≥3)从左到右的第3个数为208. 分析 从数阵看,第i行有i个数,从左到右,奇数行是从小到大排列,偶数行是从大到小排列,即可得出结论.
解答 解:从数阵看,第i行有i个数,从左到右,奇数行是从小到大排列,偶数行是从大到小排列,
所以当n为奇数时,所求数为[1+2+3+…+(n-1)]+3=$\frac{n(n-1)}{2}+3$,
当n为偶数时,所求数为$(1+2+3+…+n)-2=\frac{n(n+1)}{2}-2$.
n=20时,所求数为$\frac{20×21}{2}$-2=208,
故答案为:208.
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=|2x-1|+|x-a|,g(x)=x-1.
已知函数f(x)=|2x-1|+|x-a|,g(x)=x-1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数值域为[1,π] | B. | 此函数不单调 | C. | 此函数为偶函数 | D. | 方程f[f(x)]=x有两解 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com