
分析 本题考查的知识点是归纳推理,我们可以根据已知条件中的等式,分析等式两边的系数及指数部分与式子编号之间的关系,易得等式右边展开式中的第三项分别为:1,3,6,10,…,归纳后即可推断出a2的等式.
解答 解:由已知中的式了,我们观察后分析:
等式右边展开式中的第三项分别为:1,3,6,10,…,
即:1,1+2.1+2+3,1+2+3+4,…
根据已知可以推断:
第n(n∈N*)个等式中a2为:1+2+3+4+…+n=$\frac{n(n+1)}{2}$,
n=6时,$\frac{n(n+1)}{2}$=21,
故答案为:21
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源: 题型:解答题
 某地区业余足球运动员共有15000人,其中男运动员9000人,女运动员6000人,为调查该地区业余足球运动员每周平均踢足球占用时间的情况,采用分层抽样的方法,收集300位业务足球运动员每周平均踢足球占用时间的样本数据(单位:小时)
某地区业余足球运动员共有15000人,其中男运动员9000人,女运动员6000人,为调查该地区业余足球运动员每周平均踢足球占用时间的情况,采用分层抽样的方法,收集300位业务足球运动员每周平均踢足球占用时间的样本数据(单位:小时)| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在如图所示的几何体中,△ABC是正三角形,且EA⊥平面ABC,DB⊥平面ABC,M是AB的中点.
在如图所示的几何体中,△ABC是正三角形,且EA⊥平面ABC,DB⊥平面ABC,M是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
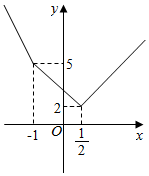 已知函数f(x)=|2x-1|+|x-a|,g(x)=x-1.
已知函数f(x)=|2x-1|+|x-a|,g(x)=x-1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
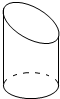 如图,一个底面半径为R的圆柱被与底面成30°二面角的平面所截,截面是一个椭圆,则该椭圆的焦距是( )
如图,一个底面半径为R的圆柱被与底面成30°二面角的平面所截,截面是一个椭圆,则该椭圆的焦距是( )| A. | R | B. | 2R | C. | $\frac{{\sqrt{3}}}{3}$R | D. | $\frac{{2\sqrt{3}}}{3}$R |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com