
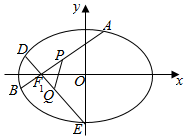
 ��֪��ԲC��$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1��a��b��0�������ҽ���ֱ�ΪF1��F2������Ϊ2����M��1��$\frac{{\sqrt{2}}}{2}}$������ԲC�ϣ�
��֪��ԲC��$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1��a��b��0�������ҽ���ֱ�ΪF1��F2������Ϊ2����M��1��$\frac{{\sqrt{2}}}{2}}$������ԲC�ϣ����� ��������֪�����õ�����a��b��c�ķ����飬��ⷽ����õ�a2��b2��ֵ������Բ���̿���
�����ɣ�1�������Բ��F1�����꣬�����ֱ��б�ʾ�����ʱ��ֱ��AB�ķ���Ϊy=k��x+1��������ֱ�߷�������Բ���̣����AB�е����꣬��-$\frac{1}{k}$����k���õ���Q�����꣬��һ���õ�PQ����ֱ�߷��̣��õ�ֱ��PQ�����㣨$-\frac{2}{3}$��0��������ֱ������һ��б�ʲ����ڣ���������ֱ֪��PQΪx�ᣬ������Ȼ�������ɴ�˵��ֱ��PQ�����㣮
��� �⣺������ԲC��$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1��a��b��0���Ľ���Ϊ2���ҵ�M��1��$\frac{{\sqrt{2}}}{2}}$������ԲC�ϣ�
��$\left\{\begin{array}{l}{c=1}\\{\frac{1}{{a}^{2}}+\frac{1}{2{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$��
��ã�a2=2��b2=1��
����ԲC�ķ���Ϊ$\frac{{x}^{2}}{2}+{y}^{2}=1$��
�����ɣ���$c=\sqrt{{a}^{2}-{b}^{2}}=\sqrt{2-1}-1$��
��F1��-1��0����
����ֱ��б�ʾ����ڣ���ֱ��AB�ķ���Ϊy=k��x+1����
������ԲC�Ĺ켣���̣��õ�����1+2k2��x2+4k2x+2k2-2=0��
��${x}_{1}+{x}_{2}=\frac{-4{k}^{2}}{1+2{k}^{2}}$��${y}_{1}+{y}_{2}=k��{x}_{1}+{x}_{2}��+2k=k\frac{-4{k}^{2}}{1+2{k}^{2}}+2k$=$\frac{2k}{1+2{k}^{2}}$��
��AB���е�����ΪP��$\frac{-2{k}^{2}}{1+2{k}^{2}}$��$\frac{k}{1+2{k}^{2}}$����
����ʽ�е�k��-$\frac{1}{k}$�������õ���Q�����꣨$-\frac{2}{{k}^{2}+2}$��$-\frac{k}{{k}^{2}+2}$����
�ɵ�P��Q������õ�ֱ��PQ�ķ���Ϊ$y+\frac{k}{{k}^{2}+2}=\frac{3k}{2��1-{k}^{2}��}��x+\frac{2}{{k}^{2}+2}��$��
��$y=\frac{3k}{2��1-{k}^{2}��}��x+\frac{2}{3}��$��
��ֱ��PQ�����㣨$-\frac{2}{3}$��0����
����ֱ������һ��б�ʲ����ڣ���������ֱ֪��PQΪx�ᣬ����������Ȼ������
��ֱ��PQ�����㣨$-\frac{2}{3}$��0����
���� ���⿼���Ĺ켣���̵�������ֱ���Ƿ��������жϷ�����ѵ����ֱ����Բ����λ�ù�ϵ��Ӧ�ã�ע�⺯���뷽��˼��ĺ������ã����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
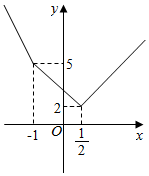 ��֪����f��x��=|2x-1|+|x-a|��g��x��=x-1��
��֪����f��x��=|2x-1|+|x-a|��g��x��=x-1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com