
| 2 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 13 |
| 25 |
| ||||
|
| 1 |
| 100 |
| ||||||||||||
|
| 24 |
| 100 |
| ||||||||||||||||
|
| 57 |
| 100 |
| ||||||||||||
|
| 18 |
| 100 |
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 18 |
| 100 |
| 57 |
| 100 |
| 24 |
| 100 |
| 1 |
| 100 |
| 26 |
| 25 |


科目:高中数学 来源: 题型:
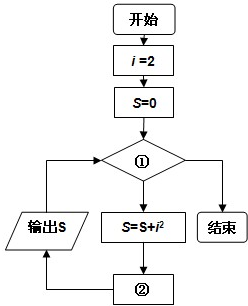 如图分别表示输出22,22+42,22+42+62,…,22+42+62+…+20142值得过程的一个程序框图,那么在图中①②分别填上( )
如图分别表示输出22,22+42,22+42+62,…,22+42+62+…+20142值得过程的一个程序框图,那么在图中①②分别填上( )| A、i≤2014,i=i+1 |
| B、i≤1007,i=i+1 |
| C、i≤2014,i=i+2 |
| D、i≤1007,i=i+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
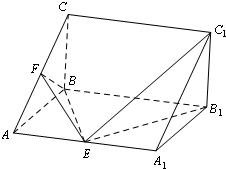 如图,在三菱柱ABC-A1B1C1中,AA1B1B为矩形,平面AA1B1B⊥平面ABC.∠ABC=90°,AB=BC=
如图,在三菱柱ABC-A1B1C1中,AA1B1B为矩形,平面AA1B1B⊥平面ABC.∠ABC=90°,AB=BC=| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、{1,2} |
| B、{1,4} |
| C、{1,3} |
| D、{2,4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com