
【题目】已知二次函数f(x)=ax2﹣4x+c的值域为[0,+∞).
(1)判断此函数的奇偶性,并说明理由;
(2)判断此函数在[ ![]() ,+∞)的单调性,并用单调性的定义证明你的结论;
,+∞)的单调性,并用单调性的定义证明你的结论;
(3)求出f(x)在[1,+∞)上的最小值g(a),并求g(a)的值域.
【答案】
(1)解:由二次函数f(x)=ax2﹣4x+c的值域为[0,+∞),得a>0且 ![]() ,
,
解得ac=4.
∵f(1)=a+c﹣4,f(﹣1)=a+c+4,a>0且c>0,从而f(﹣1)≠f(1),f(﹣1)≠﹣f(1),
∴此函数是非奇非偶函数
(2)解:函数的单调递增区间是[ ![]() ,+∞).设x1、x2是满足
,+∞).设x1、x2是满足 ![]() 的任意两个数,从而有
的任意两个数,从而有 ![]() ,∴
,∴ ![]() .又a>0,∴
.又a>0,∴ ![]() ,
,
从而 ![]() ,
,
即 ![]() ,从而f(x2)>f(x1),∴函数在[
,从而f(x2)>f(x1),∴函数在[ ![]() ,+∞)上是单调递增
,+∞)上是单调递增
(3)解:f(x)=ax2﹣4x+c,又a>0, ![]() ,x∈[1,+∞)
,x∈[1,+∞)
当 ![]() ,即0<a≤2时,最小值g(a)=f(x0)=0
,即0<a≤2时,最小值g(a)=f(x0)=0
当 ![]() ,即a>2时,最小值
,即a>2时,最小值 ![]()
综上,最小值 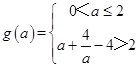
当0<a≤2时,最小值g(a)=0
当a>2时,最小值 ![]()
综上y=g(a)的值域为[0,+∞)
【解析】(1)由二次函数f(x)=ax2﹣4x+c的值域,推出ac=4,判断f(﹣1)≠f(1),f(﹣1)≠﹣f(1),得到此函数是非奇非偶函数.(2)求出函数的单调递增区间.设x1、x2是满足 ![]() 的任意两个数,列出不等式,推出f(x2)>f(x1),即可判断函数是单调递增.(3)f(x)=ax2﹣4x+c,当
的任意两个数,列出不等式,推出f(x2)>f(x1),即可判断函数是单调递增.(3)f(x)=ax2﹣4x+c,当 ![]() ,即0<a≤2时,当
,即0<a≤2时,当 ![]() ,即a>2时求出最小值即可.
,即a>2时求出最小值即可.
【考点精析】通过灵活运用二次函数的性质,掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减即可以解答此题.
上递减即可以解答此题.


科目:高中数学 来源: 题型:
【题目】如图,已知直线l:x+ ![]() y﹣c=0(c>0)为公海与领海的分界线,一艘巡逻艇在O处发现了北偏东60°海面上A处有一艘走私船,走私船正向停泊在公海上接应的走私海轮B航行,以使上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,且两者都是沿直线航行,但走私船可能向任一方向逃窜.
y﹣c=0(c>0)为公海与领海的分界线,一艘巡逻艇在O处发现了北偏东60°海面上A处有一艘走私船,走私船正向停泊在公海上接应的走私海轮B航行,以使上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,且两者都是沿直线航行,但走私船可能向任一方向逃窜. 
(1)如果走私船和巡逻船相距6海里,求走私船能被截获的点的轨迹;
(2)若O与公海的最近距离20海里,要保证在领海内捕获走私船(即不能截获走私船的区域与公海不想交).则O,A之间的最远距离是多少海里?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C: ![]() =1经过点(2,3),两条渐近线的夹角为60°,直线l交双曲线于A,B两点.
=1经过点(2,3),两条渐近线的夹角为60°,直线l交双曲线于A,B两点.
(1)求双曲线C的方程;
(2)若l过原点,P为双曲线上异于A,B的一点,且直线PA,PB的斜率kPA , kPB均存在,求证:kPAkPB为定值;
(3)若l过双曲线的右焦点F1 , 是否存在x轴上的点M(m,0),使得直线l绕点F1无论怎样转动,都有 ![]() =0成立?若存在,求出M的坐标;若不存在,请说明理由.
=0成立?若存在,求出M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (a>0,且a≠1)在R上单调递减,且关于x的方程|f(x)|=2﹣x恰好有两个不相等的实数解,则a的取值范围是( )
(a>0,且a≠1)在R上单调递减,且关于x的方程|f(x)|=2﹣x恰好有两个不相等的实数解,则a的取值范围是( )
A.(0, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]∪{
]∪{ ![]() }
}
D.[ ![]() ,
, ![]() )∪{
)∪{ ![]() }
}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{bn}的前n项和为Sn , 且对任意正整数n,都有 ![]() ;
;
(1)试证明数列{bn}是等差数列,并求其通项公式;
(2)如果等比数列{an}共有2017项,其首项与公比均为2,在数列{an}的每相邻两项ai与ai+1之间插入i个(﹣1)ibi(i∈N*)后,得到一个新数列{cn},求数列{cn}中所有项的和;
(3)如果存在n∈N* , 使不等式 ![]() 成立,若存在,求实数λ的范围,若不存在,请说明理由.
成立,若存在,求实数λ的范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,横、纵坐标均为整数的点叫做格点.若函数y=f(x)的图象恰好经过k个格点,则称函数y=f(x)为k阶格点函数.已知函数:①y=x2;②y=2sinx,③y=πx﹣1;④y=cos(x+ ![]() ).其中为一阶格点函数的序号为(注:把你认为正确论断的序号都填上)
).其中为一阶格点函数的序号为(注:把你认为正确论断的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z=lg(m2﹣2m﹣2)+(m2+3m+2)i,根据以下条件分别求实数m的值或范围.
(1)z是纯虚数;
(2)z对应的点在复平面的第二象限.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图所示的程序框图 
(1)当输入的x为2,﹣1时,分别计算输出的y值,并写出输出值y关于输入值x的函数关系式;
(2)当输出的结果为4时,求输入的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,AB=2, ![]() cos2B+5cosB﹣
cos2B+5cosB﹣ ![]() =0,且点D在线段BC上.
=0,且点D在线段BC上. 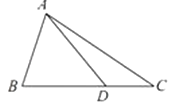
(1)若∠ADC= ![]() ,求AD的长;
,求AD的长;
(2)若BD=2DC, ![]() =4
=4 ![]() ,求△ABD的面积.
,求△ABD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com