
分析 (1)BC边的中点(1,1),利用点斜式可得可得BC边上的中线的所在的直线方程.
(2)kBC=$\frac{-1-3}{-2-4}$=$\frac{2}{3}$,可得BC边上的高线的所在的直线方程为:y-5=$-\frac{3}{2}$(x+1).
(3)直线BC的方程为:y-3=$\frac{2}{3}$(x-4),化为:2x-3y+1=0.求出点A到直线BC的距离d,|BC|即可得出面积.
解答 解:(1)BC边的中点(1,1),可得BC边上的中线的所在的直线方程为:y-1=$\frac{5-1}{-1-1}$(x-1),化为:y+2x-3=0.
(2)kBC=$\frac{-1-3}{-2-4}$=$\frac{2}{3}$,可得BC边上的高线的所在的直线方程为:y-5=$-\frac{3}{2}$(x+1),化为:3x+2y-7=0.
(3)直线BC的方程为:y-3=$\frac{2}{3}$(x-4),化为:2x-3y+1=0.
点A到直线BC的距离d=$\frac{|-2-3×5+1|}{\sqrt{{2}^{2}+(-3)^{2}}}$=$\frac{16}{\sqrt{13}}$,|BC|=$\sqrt{{6}^{2}+{4}^{2}}$=2$\sqrt{13}$.
∴S△ABC=$\frac{1}{2}×\frac{16}{\sqrt{13}}$×2$\sqrt{13}$=16.
点评 本题考查了相互垂直的直线方程斜率之间的关系、中点坐标公式、点到直线的距离公式、两点之间的距离公式、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x<1} | B. | {x|-3≤x<2} | C. | {x|-2≤x<2} | D. | {x|-3≤x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间 | (0,2) | [2,4) | [4,6) | [6,8) | 8小时以上 |
| 男生人数 | 10 | 25 | 35 | 30 | x |
| 女生人数 | 15 | 30 | 25 | y | 5 |
| 男生 | 女生 | 总计 | |
| 平均时间不超过6小时 | |||
| 平均时间超过6小时 | |||
| 总计 |
| K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$ | P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 6.635 | 7.789 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相交 | B. | 内切 | C. | 外切 | D. | 相离 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
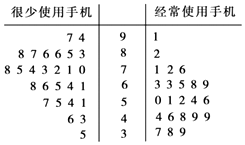 当今信息时代,众多中小学生也配上了手机.某机构为研究经常使用手机是否对学习成绩有影响,在某校高三年级50名理科生第人的10次数学考成绩中随机抽取一次成绩,用茎叶图表示如图:
当今信息时代,众多中小学生也配上了手机.某机构为研究经常使用手机是否对学习成绩有影响,在某校高三年级50名理科生第人的10次数学考成绩中随机抽取一次成绩,用茎叶图表示如图:| 及格(60及60以上) | 不及格 | 合计 | |
| 很少使用手机 | 20 | 7 | 27 |
| 经常使用手机 | 10 | 13 | 23 |
| 合计 | 30 | 20 | 50 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 |
| k0 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{12}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年四川省高二上学期期中考数学试卷(解析版) 题型:解答题
直线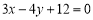 与坐标轴的交点是圆
与坐标轴的交点是圆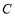 一条直径的两端点.
一条直径的两端点.
(I)求圆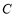 的方程;
的方程;
(II)圆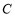 的弦
的弦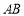 长度为
长度为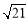 且过点
且过点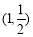 ,求弦
,求弦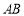 所在直线的方程.
所在直线的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com