
7个人排成一排,按下列要求各有多少种排法?
(1)其中甲不站排头,乙不站排尾;
(2)其中甲、乙、丙3人必须相邻;
(3)其中甲、乙、丙3人两两不相邻;
(4)其中甲、乙中间有且只有1人;
(5)其中甲、乙、丙按从左到右的顺序排列.
(1)3720种 (2)720种 (3)1440种 (4)1200种 (5)840种
【解析】(1)方法一(直接法):如果甲站排尾,其余6人有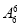 种排法,如果甲站中间5个位置中的一个,而乙不站排尾,则有
种排法,如果甲站中间5个位置中的一个,而乙不站排尾,则有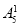

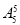 种排法,故共有排法
种排法,故共有排法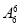 +
+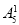
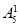
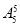 =3720种.
=3720种.
方法二(间接法):7个人排成一排有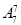 种排法,其中甲在排头有
种排法,其中甲在排头有 种排法,乙在排尾有
种排法,乙在排尾有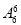 种排法,甲在排头且乙在排尾共有
种排法,甲在排头且乙在排尾共有 种排法,故共有排法
种排法,故共有排法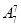 -
-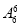 -
-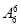 +
+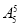 =3720种.
=3720种.
(2)(捆绑法)将甲、乙、丙捆在一起作为一个元素与其他4个元素作全排列有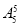 种,然后甲、乙、丙内部再作全排列有
种,然后甲、乙、丙内部再作全排列有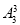 种,故有不同的排法
种,故有不同的排法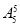
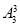 =720种.
=720种.
(3)(插空法)先排甲、乙、丙外的4人有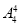 种排法,这四人之间及两端留出五个空位,然后把甲、乙、丙插入到五个空位中有
种排法,这四人之间及两端留出五个空位,然后把甲、乙、丙插入到五个空位中有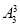 种排法,故共有
种排法,故共有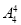
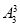 =1440种排法.
=1440种排法.
(4)甲、乙两人有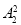 种排法,现从剩下的五人中选一个插入甲、乙中间,有
种排法,现从剩下的五人中选一个插入甲、乙中间,有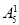 种排法,然后再将这三人看作一个元素,和其他四个元素作全排列,有
种排法,然后再将这三人看作一个元素,和其他四个元素作全排列,有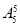 种排法,故共有
种排法,故共有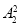
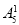
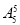 =1200种排法.
=1200种排法.
(5)七个人的全排列为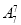 ,其中若只看甲、乙、丙不同顺序的排法有
,其中若只看甲、乙、丙不同顺序的排法有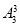 种排法,但只有一种顺序符合要求,故符合要求的不同排法有
种排法,但只有一种顺序符合要求,故符合要求的不同排法有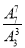 =840种.
=840种.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-6几何概型(解析版) 题型:选择题
若从区间(0,2)内随机取两个数,则这两个数的比不小于4的概率为( )
A.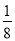 B.
B. C.
C.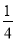 D.
D.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-3二项式定理(解析版) 题型:解答题
已知(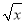 -
-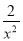 )n的展开式中,第五项与第三项的二项式系数之比为14∶3,求展开式中的常数项.
)n的展开式中,第五项与第三项的二项式系数之比为14∶3,求展开式中的常数项.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-2排列与组合(解析版) 题型:填空题
20个不加区别的小球放入1号,2号,3号的三个盒子中,要求每个盒内的球数不小于它的编号数,则不同的放法种数为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-2排列与组合(解析版) 题型:选择题
两家夫妇各带一个小孩一起到动物园游玩,购票后排队依次入园,为安全起见,首尾一定要排两位爸爸,另外,两个小孩一定要排在一起,则这6人的入园顺序排法种数为( )
A.48种 B.36种 C.24种 D.12种
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-1分类加法与分步乘法计数原理(解析版) 题型:选择题
三张卡片的正反面分别写有1和2,3和4,5和6,若将三张卡片并列,可得到不同的三位数(6不能作9用)的个数为( )
A.8 B.6 C.14 D.48
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:1-1集合的概念与运算(解析版) 题型:解答题
已知二次函数f(x)=ax2+x,若对任意x1,x2∈R,恒有2f(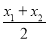 )≤f(x1)+f(x2)成立,不等式f(x)<0的解集为A.
)≤f(x1)+f(x2)成立,不等式f(x)<0的解集为A.
(1)求集合A;
(2)设集合B={x||x+4|<a},若集合B是集合A的子集,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮考前特训:创新问题专项训练2(解析版) 题型:填空题
若存在实常数k和b,使得函数f(x)和g(x)对其定义域上的任意实数x分别满足:f(x)≥kx+b和g(x)≤kx+b,则称直线l:y=kx+b为f(x)和g(x)的“隔离直线”.已知h(x)=x2,φ(x)=2eln x(其中e为自然对数的底数),根据你的数学知识,推断h(x)与φ(x)间的隔离直线方程为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学理一轮配套特训:7-1空间几何体结构及三视图和直观图(解析版) 题型:选择题
某几何体的三视图如图所示,且该几何体的体积是2,则正(主)视图的面积等于( )
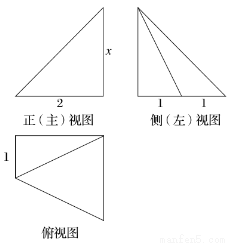
A.2 B.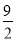 C.
C. D.3
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com