
已知二次函数f(x)=ax2+x,若对任意x1,x2∈R,恒有2f(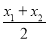 )≤f(x1)+f(x2)成立,不等式f(x)<0的解集为A.
)≤f(x1)+f(x2)成立,不等式f(x)<0的解集为A.
(1)求集合A;
(2)设集合B={x||x+4|<a},若集合B是集合A的子集,求a的取值范围.
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-5古典概型(解析版) 题型:填空题
从1到10这十个自然数中随机取三个数,则其中一个数是另两个数之和的概率是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-2排列与组合(解析版) 题型:选择题
某小区有排成一排的7个车位,现有3辆不同型号的车需要停放,如果要求剩余的4个车位连在一起,那么不同的停放方法的种数为( )
A.8 B.16 C.24 D.32
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-1分类加法与分步乘法计数原理(解析版) 题型:解答题
7个人排成一排,按下列要求各有多少种排法?
(1)其中甲不站排头,乙不站排尾;
(2)其中甲、乙、丙3人必须相邻;
(3)其中甲、乙、丙3人两两不相邻;
(4)其中甲、乙中间有且只有1人;
(5)其中甲、乙、丙按从左到右的顺序排列.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-1分类加法与分步乘法计数原理(解析版) 题型:选择题
5位同学站成一排准备照相的时候,有两位老师碰巧路过,同学们强烈要求与老师合影留念,如果5位同学顺序一定,那么两位老师与同学们站成一排照相的站法总数为( )
A.6 B.20 C.30 D.42
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:1-1集合的概念与运算(解析版) 题型:解答题
已知集合A={x|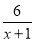 ≥1,x∈R},B={x|x2-2x-m<0}.
≥1,x∈R},B={x|x2-2x-m<0}.
(1)当m=3时,求A∩(∁RB);
(2)若A∩B={x|-1<x<4},求实数m的值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:1-1集合的概念与运算(解析版) 题型:选择题
如图,已知R是实数集,集合A={x|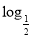 (x-1)>0},B={x|
(x-1)>0},B={x|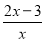 <0},则阴影部分表示的集合是( )
<0},则阴影部分表示的集合是( )
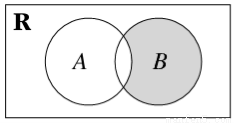
A.[0,1] B.[0,1) C.(0,1) D.(0,1]
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮考前特训:创新问题专项训练1(解析版) 题型:填空题
若从集合 ,
, ,3,4中随机抽取一个数记为a,从集合{-1,1,-2,2}中随机抽取一个数记为b,则函数f(x)=ax+b(a>0,a≠1)的图像经过第三象限的概率是________.
,3,4中随机抽取一个数记为a,从集合{-1,1,-2,2}中随机抽取一个数记为b,则函数f(x)=ax+b(a>0,a≠1)的图像经过第三象限的概率是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学理一轮配套特训:6-3二元一次不等式及简单的线性规划(解析版) 题型:填空题
若x,y满足条件 ,当且仅当x=y=3时,z=ax-y取得最小值,则实数a的取值范围是________.
,当且仅当x=y=3时,z=ax-y取得最小值,则实数a的取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com