
已知 ,且
,且 ,求
,求 的最小值.某同学做如下解答:
的最小值.某同学做如下解答:
因为  ,所以
,所以 ┄①,
┄①, ┄②,
┄②,
① ②得
②得  ,所以
,所以  的最小值为24.
的最小值为24.
判断该同学解答是否正确,若不正确,请在以下空格内填写正确的最小值;若正确,请在以下空格内填写取得最小值时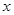 、
、 的值. .
的值. .
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com