
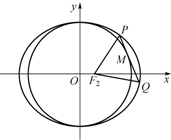
 已知椭圆的长轴长为6,离心率为$\frac{1}{3}$,F2为椭圆的右焦点.
已知椭圆的长轴长为6,离心率为$\frac{1}{3}$,F2为椭圆的右焦点.分析 (Ⅰ)由题意可知:2a=6,$e=\frac{c}{a}=\frac{1}{3}$,求得a和c的值,由b2=a2-c2,求得b,写出椭圆方程;
(Ⅱ)设P(x1,y1),Q(x2,y2),分别求出|F2P|,|F2Q|,结合相切的条件可得|PM|2=|OP|2-|OM|2,可得$|{P{F_2}}|+|{PM}|=3-\frac{1}{3}{x_1}+\frac{1}{3}{x_1}=3$,同理|QF2|+|QM|=3,即可证明;
解答 解:(I)根据已知,设椭圆的标准方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,
∴2a=6,a=3,$e=\frac{c}{a}=\frac{1}{3}$,c=1;
b2=a2-c2=8,
$\frac{x^2}{9}+\frac{y^2}{8}=1$(4分)
(II)△PF2Q的周长是定值,
设P(x1,y1),Q(x2,y2),则$\frac{x_1^2}{9}+\frac{y_1^2}{8}=1$,
$|{P{F_2}}|=\sqrt{{{({{x_1}-1})}^2}+y_1^2}=\sqrt{{{({{x_1}-1})}^2}+8(1-\frac{x_1^2}{9})}=\sqrt{{{(\frac{x_1}{3}-3)}^2}}$,
∵0<x1<3,
∴$|{P{F_2}}|=3-\frac{x_1}{3}$,(7分)
在圆中,M是切点,
∴$|{PM}|=\sqrt{|OP{|^2}-|OM{|^2}}=\sqrt{x_1^2+y_1^2-8}=\sqrt{x_1^2+8(1-\frac{x_1^2}{9})-8}=\frac{1}{3}{x_1}$,(11分)
∴$|{P{F_2}}|+|{PM}|=3-\frac{1}{3}{x_1}+\frac{1}{3}{x_1}=3$,
同理|QF2|+|QM|=3,(13分)
∴|F2P|+|F2Q|+|PQ|=3+3=6,
因此△PF2Q的周长是定值6.…(14分)
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、弦长公式、直线与圆相切性质、勾股定理、三角形的周长问题,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | S1+2S2=3S3 | B. | $\sqrt{{S}_{1}}$+$\sqrt{2{S}_{2}}$=$\sqrt{3{S}_{3}}$ | C. | $\sqrt{{S}_{1}}$+2$\sqrt{{S}_{2}}$=3$\sqrt{{S}_{3}}$ | D. | $\sqrt{{S}_{1}}$+4$\sqrt{{S}_{2}}$=9$\sqrt{{S}_{3}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
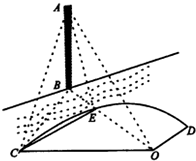 如图,河的一侧是以O为圆形,半径为80$\sqrt{3}$米的扇形区域OCD,河的另一侧有一建筑物AB垂直于水平面,假设扇形OCD与点B处于同一水平面,记OB与$\widehat{CD}$的交点为E,若在点C,点O和点E处看到点A的仰角分别为45°,30°和60°,则∠CBO的余弦值为$\frac{4\sqrt{3}}{9}$.
如图,河的一侧是以O为圆形,半径为80$\sqrt{3}$米的扇形区域OCD,河的另一侧有一建筑物AB垂直于水平面,假设扇形OCD与点B处于同一水平面,记OB与$\widehat{CD}$的交点为E,若在点C,点O和点E处看到点A的仰角分别为45°,30°和60°,则∠CBO的余弦值为$\frac{4\sqrt{3}}{9}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 椭圆的一部分 | B. | 双曲线的一部分 | C. | 抛物线的一部分 | D. | 直线的一部分 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com