Question

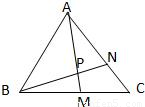
在△ABC中，点M是BC的中点，△AMC的三边长是连续三个正整数，且tan∠C=cot∠BAM．
（Ⅰ）判断△ABC的形状；
（Ⅱ）求∠BAC的余弦值．

Answer 1

分析：（Ⅰ）假设∠BAM=α，∠MAC=β，根据正弦定理可找到α，β与B，C的正弦之间的关系，进而再由诱导公式可确定α与β的关系．
（Ⅱ）先设出3个连续的整数，再由勾股定理确定关系，根据余弦定理和二倍角公式可求出角BAC的余弦值．

解答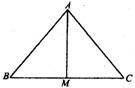：解：（Ⅰ）设∠BAM=α，∠MAC=β，
则由tanC=cotα得α+C=90°∴β+B=90°
△ABM中，由正弦定理得

BM

sinα

=

AM

sinB

，即

sinB

sinα

=

AM

MB

．
同理得

sinC

sinβ

=

AM

MC

，
∵MB=MC，∴

sinB

sinα

=

sinC

sinβ

，
∴sinαsinC=sinβsinB∵α+C=90°，β+B=90°，∴sinαcosα=sinβcosβ
即sin2α=sin2β，∴α=β或α+β=90°
当α+β=90°时，AM=

1

2

BC=MC，
与△AMC的三边长是连续三个正整数矛盾，
∴α=β，∴∠B=∠C，∴△ABC是等腰三角形．

（Ⅱ）在直角三角形AMC中，设两直角边分别为n，n-1，斜边为n+1，
由（n+1）²=n²+（n-1）²得n=4，
由余弦定理或二倍角公式得cos∠BAC=

7

25

．
或cos∠BAC=-

7

25

．

点评：本题主要考查正弦定理、余弦定理的应用．三角函数部分公式比较多，一定要强化记忆．