练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    某工厂对一批产品进行了抽样检测．如图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，已知样本中产品净重小于100克的个数是36，则样本中净重大于或等于98克并且小于104克的产品的个数是（　　）
    A、90B、75C、60D、45
    考点：频率分布直方图
    专题：概率与统计
    分析：根据频率分布直方图，先求出样本容量，再计算样本中净重大于或等于98克并且小于104克的频率与频率．
    解答： 解：根据频率分布直方图，得；
    样本中产品净重小于100克的频率是
    （0.05+0.10）×2=0.30，
    ∴样本容量是
    36
    0.30
    =120；
    ∴样本中净重大于或等于98克并且小于104克的频率是
    1-（0.05+0.075）×2=1-0.25=0.75，
    ∴对应产品的个数是
    120×0.75=90．
    故选：A．
    点评：本题考查了频率分布直方图的应用问题，解题时应利用频率=
    频数
    样本容量
    进行解答，是基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知抛物线y2=2x，过点Q（2，1）作一条直线交抛物线于A、B两点，求弦AB中点的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

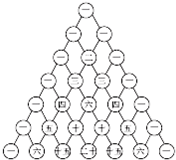    如图中的杨辉三角最早出现于我国南宋数学家杨辉1261年所著的《详解九章算法》．它有很多奇妙的性质，如每个数等于它肩上两数之和．记图中从上到下第i行从左到右第j个数为（i，j）．数列{an}的前n项和Sn=（n+2，3），n∈N*．
    （I）求数列{an}的通项公式；
    （Ⅱ）设bn=
    1
    Sn
    ，数列{bn}的前n项和为Tn证明：1≤Tn＜2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    阅读如图所示的程序框图，运行相应的程序，若输入n的值为100，则输出S的值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知某地区中小学生人数和近视情况如表所示：
    年级人数近视率
    小学350010%
    初中450030%
    高中200050%
    为了解该地区中小学生的近视形成原因，用分层抽样的方法抽取2%的学生进行调查，则：
    （Ⅰ）样本容量为
     
    ；
    抽取的高中生中，近视人数为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出下列命题：
    ①存在实数α，使sinα•cosα=1；
    ②函数y=sin(
    3
    2
    π+x)    是偶函数；
    ③f(x)=4sin(2x+
    π
    3
    )(x∈R)      图象关于(-
    π
    6
    ，0)    对称；
    ④若α、β是第一象限的角，且α＞β，则sinα＞sinβ；
    其中正确命题的序号是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=
    1
    x-2
    ，则当x∈[3，5）时函数的值域为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若函数f（x）在R上是单调递减的奇函数，则下列关系式成立的是（　　）
    A、f（3）＜f（4）
    B、f（3）＜-f（-4）
    C、-f（-3）＜f（-4）
    D、f（-3）＞f（-4）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，正方形DEFM内接于△ABC，且点D，E在AB，AC上，点F，M在BC上，∠A=90°，S△CEF=1，S△BMD=4，求S△ABC．

    查看答案和解析>>

    同步练习册答案