
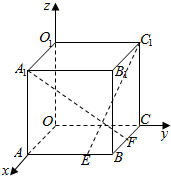
 如图,在棱长为a的正方体OABC-O1A1B1C1中,E,F分别是棱AB、BC上的动点,且AE=BF=x,其中0≤x≤a,以O为原点建立空间直角坐标系O-xyz.
如图,在棱长为a的正方体OABC-O1A1B1C1中,E,F分别是棱AB、BC上的动点,且AE=BF=x,其中0≤x≤a,以O为原点建立空间直角坐标系O-xyz.分析 (1)在空间直角坐标中结合正方体结构特征,能求出E,F的坐标.
(2)求出$\overrightarrow{{{A}_{1}F}^{\;}}$=(-x,a,-a),$\overrightarrow{{C}_{1}E}$=(a,x-a,-a),利用向量法能证明A1F⊥C1E.
(3)由A1、E、F、C1四点共面,得到$\overrightarrow{EF}$∥$\overrightarrow{{A}_{1}{C}_{1}}$,从而E,F,分别AB,BC的中点,由此能证明$\overrightarrow{{A}_{1}F}$=$\frac{1}{2}$$\overrightarrow{{A}_{1}{C}_{1}}$+$\overrightarrow{{A}_{1}E}$.
解答 解:(1) ∵在棱长为a的正方体OABC-O1A1B1C1中,E,F分别是棱AB、BC上的动点,
∵在棱长为a的正方体OABC-O1A1B1C1中,E,F分别是棱AB、BC上的动点,
且AE=BF=x,其中0≤x≤a,以O为原点建立空间直角坐标系O-xyz,
∴E(a,x,0),F(a-x,a,0).
证明:(2)A1(a,0,a),C1(0,a,a),
$\overrightarrow{{{A}_{1}F}^{\;}}$=(-x,a,-a),$\overrightarrow{{C}_{1}E}$=(a,x-a,-a),
∵$\overrightarrow{{A}_{1}F}•\overrightarrow{{C}_{1}E}$=-ax+ax-a2+a2=0,
∴A1F⊥C1E.
(3)∵E(a,x,0),F(a-x,a,0),A1、E、F、C1四点共面,
$\overrightarrow{EF}$=(-x,a-x,0),$\overrightarrow{{A}_{1}{C}_{1}}$=(-a,a,0),
∴$\overrightarrow{EF}$∥$\overrightarrow{{A}_{1}{C}_{1}}$,∴$\frac{-x}{-a}=\frac{a-x}{a}$,解得x=$\frac{a}{2}$,
∴E,F,分别AB,BC的中点,
∴$\overrightarrow{{A}_{1}F}$=$\frac{1}{2}$$\overrightarrow{{A}_{1}{C}_{1}}$+$\overrightarrow{{A}_{1}E}$.
点评 本题考查空间直角坐标系中点的坐标的求法,考查两直线垂直的证明,考查向量相等的证明,是中档题,解题时要认真审题,注意向量法的合理运用.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{1}{100}$ex | B. | y=100lnx | C. | y=x100 | D. | y=100•2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com