
分析 根据题意,画出图形,结合图形,利用空间向量的线性运算,即可用$\overrightarrow{CA}=\overrightarrow a$,$\overrightarrow{CB}=\overrightarrow b$,$\overrightarrow{C{C_1}}=\overrightarrow c$表示出$\overrightarrow{{A_1}B}$.
解答 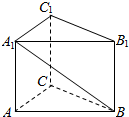 解:如图所示,
解:如图所示,
三棱柱ABC-A1B1C1中,且$\overrightarrow{CA}=\overrightarrow a$,$\overrightarrow{CB}=\overrightarrow b$,$\overrightarrow{C{C_1}}=\overrightarrow c$,
所以$\overrightarrow{{A_1}B}$=$\overrightarrow{{A}_{1}A}$+$\overrightarrow{AC}$+$\overrightarrow{CB}$
=$\overrightarrow{{C}_{1}C}$-$\overrightarrow{CA}$+$\overrightarrow{CB}$
=-$\overrightarrow{CA}$+$\overrightarrow{CB}$-$\overrightarrow{{CC}_{1}}$
=-$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$.
故答案为:-$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$.
点评 本题考查了空间向量的线性表示与运算问题,是基础题目.


 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
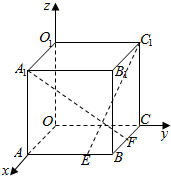 如图,在棱长为a的正方体OABC-O1A1B1C1中,E,F分别是棱AB、BC上的动点,且AE=BF=x,其中0≤x≤a,以O为原点建立空间直角坐标系O-xyz.
如图,在棱长为a的正方体OABC-O1A1B1C1中,E,F分别是棱AB、BC上的动点,且AE=BF=x,其中0≤x≤a,以O为原点建立空间直角坐标系O-xyz.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{3}$π | B. | 12π | C. | 8π | D. | 4$\sqrt{6}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com