
分析 (1)由题意:求函数的定义域得到集合A,在根据集合的基本运算求解A∪B,(∁RB)∩A;
(2)因为2a∈A,log2(2a-1)∈B,即A是2a的值域,B是log2(2a-1)的值域,即可求解a的范围.
解答 解:(1)函数f(x)=lg[log${\;}_{\frac{1}{2}}}$(${\frac{1}{2}$x-1)]的定义域是集合A;
函数f(x)的定义域满足.${log_{\frac{1}{2}}}(\frac{1}{2}x-1)>0$,
∴$0<\frac{1}{2}x-1<1$,
∴2<x<4,
∴集合A=(2,4);
集合B={x|x<1,或x≥3}.即B=(-∞,1)∪[3,+∞),
∴∁RB=[1,3),
故得∴A∪B=(-∞,1)∪(2,+∞);
(∁RB)∩A=(2,3).
(2)由(1)得A=(2,4);B=(-∞,1)∪[3,+∞),
∵2a∈A,
∴2<2a<4,
解得:1<a<2,
又∵log2(2a-1)∈B,
∴log2(2a-1)<1或log2(2a-1)≥3,
∴0<2a-1<2或2a-1≥8,
解得$\frac{1}{2}<a<\frac{3}{2}或a≥\frac{9}{2}$
∴$1<a<\frac{3}{2}$.
所以实数a的取值范围是(1,$\frac{3}{2}$).
点评 本题考查了对函数的定义域求法和集合的基本运算,对数,指数的计算问题.属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | (-2,0)∪(2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-2,0)∪(0,2) | D. | (-∞,-2)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,2) | C. | (1,0) | D. | (2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?c>0,方程x2-x+c=0无解 | B. | ?c≤0,方程x2-x+c=0有解 | ||
| C. | ?c>0,方程x2-x+c=0无解 | D. | ?c<0,方程x2-x+c=0有解 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
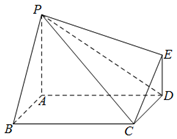 如图,四边形ABCD为矩形,PA⊥平面ABCD,DE∥PA.
如图,四边形ABCD为矩形,PA⊥平面ABCD,DE∥PA.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com