
【题目】如图,四棱锥![]() 的底面
的底面![]() 为直角梯形,
为直角梯形,![]() ,且
,且![]() ,
,![]() ,
,![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为等边三角形,
为等边三角形,![]() 是棱
是棱![]() 上的一点,设
上的一点,设![]() (
(![]() 与
与![]() 不重合).
不重合).
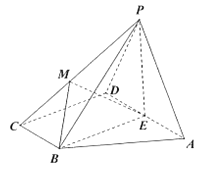
(1)若![]() 平面
平面![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,求二面角
时,求二面角![]() 的大小.
的大小.
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,点
,点![]() 满足
满足![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]() .斜率为
.斜率为![]() 的直线
的直线![]() 过点
过点![]() ,且与轨迹
,且与轨迹![]() 相交于
相交于![]() 两点.
两点.
(1)求轨迹![]() 的方程;
的方程;
(2)求斜率![]() 的取值范围;
的取值范围;
(3)在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得无论直线
,使得无论直线![]() 绕点
绕点![]() 怎样转动,总有
怎样转动,总有![]() 成立?如果存在,求出定点
成立?如果存在,求出定点![]() ;如果不存在,请说明理由.
;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体.![]() 分别为
分别为![]() 的中点,
的中点,![]() 为弧
为弧![]() 的中点,
的中点,![]() 为弧
为弧![]() 的中点.
的中点.
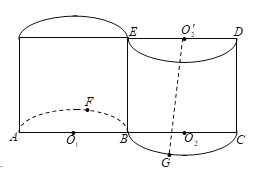
(1)求直线![]() 与底面
与底面![]() 所成的角的大小;
所成的角的大小;
(2)求异面直线![]() 与
与![]() 所成的角的大小(结果用反三角函数值表示).
所成的角的大小(结果用反三角函数值表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三角形![]() 的边长为
的边长为![]() ,
,![]() 、
、![]() 、
、![]() 分别为各边的中点,将△
分别为各边的中点,将△![]() 沿
沿![]() 、
、![]() 、
、![]() 折叠,使
折叠,使![]() 、
、![]() 、
、![]() 三点重合,构成三棱锥
三点重合,构成三棱锥![]() .
.
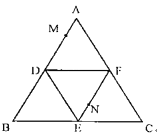
(1)求平面![]() 与底面
与底面![]() 所成二面角的余弦值;
所成二面角的余弦值;
(2)设点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,
上,![]() (
(![]() 为变量) ;
为变量) ;
①当![]() 为何值时,
为何值时,![]() 为异面直线
为异面直线![]() 与
与![]() 的公垂线段? 请证明你的结论
的公垂线段? 请证明你的结论
②设异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,异面直线
,异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为有效促进我市体育产业和旅游产业有机融合,提高我市的知名度,更好地宣传萍乡武功山,并通过赛事向社会各界传播健康、低碳、绿色、环保的运动理念。在今年9月21日第九届环鄱阳湖国际自行车大赛第九站比赛在我市武功山举行。在这次89.5公里的自行车个人赛中,其中25名参赛选手的成绩(单位:分钟)的茎叶图如图所示:
14 | 0 | 1 | 2 | 3 | 5 | 6 | 6 | 6 | 6 | 8 | 9 |
15 | 0 | 2 | 3 | 4 | 5 | 5 | 5 | 7 | 9 | ||
16 | 0 | 0 | 5 | 6 | 7 |