
分析 (Ⅰ)函数f(x)图象上点M处切线斜率为${f^'}(x)=\frac{lnx-1}{{{{ln}^2}x}}=-\frac{1}{{{{ln}^2}x}}+\frac{1}{lnx}$,利用x∈(1,e2],即可求函数f(x)图象上点M处切线斜率的最大值;
(Ⅱ) h(x)在点(e,h(e))处的切线l与直线x-y-2=0垂直,h′(e)=a=-1,h(e)=1,即可求切线l方程.
解答 解:(Ⅰ)设切点M(x,f(x)),则x∈(1,e2].
函数f(x)图象上点M处切线斜率为${f^'}(x)=\frac{lnx-1}{{{{ln}^2}x}}=-\frac{1}{{{{ln}^2}x}}+\frac{1}{lnx}$…(2分)
∵$x∈({1,\left.{e^2}]}\right.,\frac{1}{lnx}∈[{\frac{1}{2}}\right.,\left.{+∞})$,…(4分)
∴${f^'}(x)=-{({\frac{1}{lnx}-\frac{1}{2}})^2}+\frac{1}{4}$,
∴$当\frac{1}{lnx}=\frac{1}{2}时,即x={e^2},{f^'}{(x)_{max}}=\frac{1}{4}$…(6分)
(Ⅱ)∵$h(x)=\frac{x}{lnx}+ax+1$,${h^,}(x)=\frac{lnx-1}{{{{ln}^2}x}}+a$,…(8分)
又h(x)在点(e,h(e))处的切线l与直线x-y-2=0垂直.
∴h′(e)=a=-1,h(e)=1,…(10分)
切线l的方程为x+y-1-e=0…(12分)
点评 本题考查导数知识的运用,考查导数的几何意义,考查学生分析解决问题的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 90° | C. | 105° | D. | 75° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
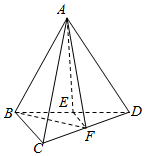 如如,在三棱锥A-BCD中,AB=AD,BC⊥CD,平面ABD⊥平面BCD,点E,F分别是BD,CD的中点.
如如,在三棱锥A-BCD中,AB=AD,BC⊥CD,平面ABD⊥平面BCD,点E,F分别是BD,CD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com