
 已知PA⊥平面ABCD,CD⊥AD,BA⊥AD,CD=AD=AP=4,AB=1.
已知PA⊥平面ABCD,CD⊥AD,BA⊥AD,CD=AD=AP=4,AB=1.分析 (1)利用面面垂直证明线面垂直.(2)合理建系写出对应坐标,充分理解BM⊥AC的意义求得M点坐标
解答  (1)证明:
(1)证明:
因为PA⊥平面ABCD,PA?平面ADP,
所以平面ADP⊥平面ABCD.…(2分)
又因为平面ADP∩平面ABCD=AD,CD⊥AD,
所以CD⊥平面ADP.…(4分)
(2)AD,AP,AB两两垂直,建立如图所示空间坐标系,
则A(0,0,0),B(0,0,1),
C(4,0,4),P(0,4,0),$\overrightarrow{AB}=(0,0,1),\overrightarrow{AC}=(4,0,4)$$\overrightarrow{AP}=(0,4,0),\overrightarrow{PC}=(4,-4,4)$.…(6分)
设M(x,y,z),$\overrightarrow{PM}=λ\overrightarrow{PC}(0≤λ≤1)$,$\overrightarrow{PM}=(x,y-4,z)$.
所(x,y-4,z)=λ(4,-4,4)$\left\{\begin{array}{l}{x=4λ}\\{y=4-4λ}\\{z=4λ}\end{array}\right.$,$M(4λ,4-4λ,4λ),\overrightarrow{BM}=(4λ,4-4λ,4λ-1)$.
因为BM⊥AC,所以$\overrightarrow{BM}•\overrightarrow{AC}=0$.,(4λ,4-4λ,4λ-1)•(4,0,4)=0,解$λ=\frac{1}{8}$,
所以M=$(\frac{1}{2},\frac{7}{2},\frac{1}{2})$,.…(8分)
设$\overrightarrow{\\;n}=({x}_{1},{y}_{1},{z}_{1})$为平面ABM的法向量,
则$\left\{\begin{array}{l}{\overrightarrow{\\;{n}_{1}}•\overrightarrow{AB}=0}\\{\overrightarrow{n}•\overrightarrow{AM}=0}\end{array}\right.$,又因为$\overrightarrow{AB}=(0,0,1),\overrightarrow{AM}=(\frac{1}{2},\frac{7}{2},\frac{1}{2})$
所以$\left\{\begin{array}{l}{\\;{z}_{1}=0}\\{\frac{1}{2}{x}_{1}+\frac{7}{2}{y}_{1}+\frac{1}{2}{z}_{1}=0}\end{array}\right.$.
令${y}_{1}=1\\;得\overrightarrow{{n}_{1}}=(-7,1,0)$为平面ABM的一个法向量.
又因为AP⊥平面ABC,所以$\overrightarrow{{n}_{2}}=(0,4,0)$为平面ABC的一个法向量.…(10分)
$cos<\overrightarrow{{n}_{1}},\overrightarrow{{n}_{2}}>=\frac{\overrightarrow{n1}•\overrightarrow{{n}_{2}}}{|\overrightarrow{{n}_{1}}||\overrightarrow{{n}_{2}}|}$=$\frac{\sqrt{2}}{10}$,
所以二面角C-AB-M的余弦值为$\frac{\sqrt{2}}{10}$.…(12分)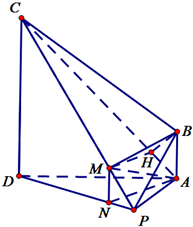
法2:
在平面ABCD内过点B作BH⊥AC于H,
在平面ACP内过点H作HM∥AP交PC于点M,连接MB …(6分),
因为AP⊥平面ABCD,
所以HM⊥平面ABCD.
又因为AC?平面ABCD,
所以HM⊥AC.
又BH∩HM=H,BH?平面BHM,HM?平面BHM,
所以AC⊥平面BHM.
所以AC⊥BM,点M即为所求点.…(8分)
在直角△ABH中,AH=$\frac{\sqrt{2}}{2}AB=\frac{\sqrt{2}}{2}$,
又AC=$\sqrt{C{D}^{2}+D{A}^{2}}=4\sqrt{2}$,所以$\frac{AH}{AC}=\frac{1}{8}$.
又HM∥AP,所以在△ACP中,$\frac{PM}{PC}=\frac{1}{8}$.
在平面PCD内过点M作MN∥CD交DP于点N,则在△PCD中,$\frac{PN}{PD}=\frac{1}{8}$.
因为AB∥CD,所以MN∥BA.
连接AN,由(1)知CD⊥平面ADP,所以AB⊥平面ADP.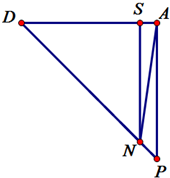
所以AB⊥AD,AB⊥AN.
所以∠DAN为二面角C-AB-M的平面角.…(10分)
在△PAD中,过点N作NS∥PA交DA于S,则$\frac{AS}{AD}=\frac{1}{8}$,
所以AS=$\frac{1}{2}$,NS=$\frac{7}{8}PA=\frac{7}{2}$,所以NA=$\frac{5\sqrt{2}}{2}$.
所以$cos∠SAN=\frac{AS}{NA}=\frac{\sqrt{2}}{10}$.
所以二面角C-AB-M的余弦值为$\frac{\sqrt{2}}{10}$.…(12分)
点评 本题考查利用面面垂直证明线面垂直,是证明题常见题型.在未知某点坐标时利用条件求出点的坐标时该题的难点也是高考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 如图:我国海监船沿东西方向的海岸线l上的M、N处停泊着我国渔民的捕鱼船,MN=1km,我国海监船在点M的正东方向30km的点O处,观测到一日系船正匀速直线航向我国海域,当该日系船位于点O的北偏东30°方向上的A处(OA=20$\sqrt{3}$km)时,我方开始向日方喊话,但该日系船仍匀速航行,40min后,又测该日系船位于点O的正北方向上的点B处,且OB=20km.(参考数据:$\sqrt{3}$≈1.732)
如图:我国海监船沿东西方向的海岸线l上的M、N处停泊着我国渔民的捕鱼船,MN=1km,我国海监船在点M的正东方向30km的点O处,观测到一日系船正匀速直线航向我国海域,当该日系船位于点O的北偏东30°方向上的A处(OA=20$\sqrt{3}$km)时,我方开始向日方喊话,但该日系船仍匀速航行,40min后,又测该日系船位于点O的正北方向上的点B处,且OB=20km.(参考数据:$\sqrt{3}$≈1.732)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | $8\sqrt{2}$ | D. | $10\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 对某校高二年级学生暑期参加社会实践次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社会实践的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如图:
对某校高二年级学生暑期参加社会实践次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社会实践的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如图:| 分组 | 频数 | 频率 |
| [10,15) | 20 | 0.25 |
| [15,20) | 48 | n |
| [20,25) | m | p |
| [25,30) | 4 | 0.05 |
| 合计 | M | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点,求证:
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$a2 | B. | -$\frac{3}{4}$a2 | C. | $\frac{3}{4}$a2 | D. | $\frac{3}{2}$a2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com