Question

19．直线l过抛物线C：y²=4x的焦点，且与抛物线C交于A、B两点，过点A、B分别向抛物线的准线作垂线，垂足分别为P、Q，则四边形APQB的面积的最小值为（　　）

• A． 6
• B． 8
• C． $8\sqrt{2}$
• D． $10\sqrt{2}$

Answer 1

分析 分直线AB的斜率不存在与存在两种情况讨论，当直线AB的斜率存在时，利用韦达定理、双曲线的第二定义、函数的单调性即得结论．

解答 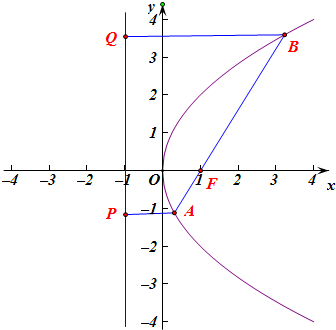解：如图，F（1，0），线面对直线AB的斜率进行讨论：
①当直线AB的斜率不存在时，此时直线AB的方程为：x=1，
∴A（1，-2），B（1，2），
此时P（-1，-2），Q（-1，2），
∴S_{四边形APQB}=AP•PQ=2×4=8；
②当直线AB的斜率存在时，设直线AB的方程为：y=k（x-1），
记A（x₁，y₁），B（x₂，y₂），
联立直线与抛物线方程得$\frac{k}{4}$y²-y-k=0，
由韦达定理可得y₁+y₂=$\frac{4}{k}$，y₁y₂=-4，
∴（y₁-y₂）²=（y₁+y₂）²-4y₁•y₂=$\frac{16}{{k}^{2}}$+16，
又∵（x₁-x₂）²=[（x₁-1）-（x₂-1）]²=[$\frac{{y}_{1}{-y}_{2}}{k}$]²=$\frac{16-16{k}^{2}}{{k}^{4}}$，
∴AB=$\sqrt{（{x}_{1}-{x}_{2}）^{2}+（{y}_{1}-{y}_{2}）^{2}}$=$\sqrt{\frac{16}{{k}^{4}}+16}$，
∴S_{四边形APQB}=$\frac{1}{2}$（AP+BQ）•PQ=$\frac{1}{2}$AB•PQ=$\frac{1}{2}$•$\sqrt{\frac{16}{{k}^{4}}+16}$•$\sqrt{\frac{16}{{k}^{2}}+16}$，
令t=$\frac{1}{{k}^{2}}$，则S_{四边形APQB}=$\frac{1}{2}$•16•$\sqrt{（{t}^{2}+1）（t+1）}$=8$\sqrt{{t}^{3}+{t}^{2}+t+1}$，
记f（t）=t³+t²+t+1，则f′（t）=3t²+2t+1＞0，
即f（t）在（0，+∞）上单调递增，
∴S_{四边形APQB}＞8；
综上所述，当直线AB的斜率不存在时，四边形APQB的面积最小，
故选：B．

点评 本题是一道直线与双曲线的综合题，涉及到韦达定理、双曲线的第二定义、函数的单调性等知识，考查计算能力，注意解题方法的积累，属于中档题．