练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．复数z满足（z-2i）（1+i）=|1+$\sqrt{3}i$|（i为虚数单位），则复数z=（　　）
    A．1+iB．1-iC．1D．-1

    分析 求出复数的模，利用复数的除法运算法则，化简求解即可．

    解答 解：复数z满足（z-2i）（1+i）=|1+$\sqrt{3}i$|=2，
    z=$\frac{2}{1+i}+2i$=$\frac{2（1-i）}{（1+i）（1-i）}+2i$=1+i．
    故选：A．

    点评 本题考查复数的基本运算，复数的模的求法，考查计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    10．已知命题p：“将函数y=sin（2x+θ）的图象沿x轴向右平移$\frac{π}{16}$个单位后，得到一个关于y轴对称的图象”，命题q“θ=kπ+$\frac{5π}{8}$（k∈Z）“，则p是q的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．如图：我国海监船沿东西方向的海岸线l上的M、N处停泊着我国渔民的捕鱼船，MN=1km，我国海监船在点M的正东方向30km的点O处，观测到一日系船正匀速直线航向我国海域，当该日系船位于点O的北偏东30°方向上的A处（OA=20$\sqrt{3}$km）时，我方开始向日方喊话，但该日系船仍匀速航行，40min后，又测该日系船位于点O的正北方向上的点B处，且OB=20km．（参考数据：$\sqrt{3}$≈1.732）
    （1）求该日系船航行的速度．
    （2）若该日系船不改变方向继续航行，则其是否会正好行至我国捕鱼船停泊处（即M、N处）？请经过计算说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．求过点（3，-2）且与椭圆4x2+9y2=36有相同焦点的椭圆方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

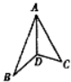    2．在正三角形ABC中，AD⊥BC于D，沿AD折成二面角B-AD-C后，BC=$\frac{1}{2}$AB，这时二面角B-AD-C的大小为60°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．在四面体P-ABC中，PA=PB=PC=1，∠APB=∠BPC=∠CPA=90°则该四面体P-ABC的外接球的表面积为3π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．直线l过抛物线C：y2=4x的焦点，且与抛物线C交于A、B两点，过点A、B分别向抛物线的准线作垂线，垂足分别为P、Q，则四边形APQB的面积的最小值为（　　）
    A．6B．8C．$8\sqrt{2}$D．$10\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．对某校高二年级学生暑期参加社会实践次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社会实践的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如图：
    分组频数频率
    [10，15）200.25
    [15，20）48n
    [20，25）mp
    [25，30）40.05
    合计M1
    （1）求出表中M，p及图中a的值；
    （2）在所取样本中，从参加社会实践的次数不少于20次的学生中任选3人，记参加社会实践次数在区间[25，30）内的人数为X，求X的分布列和期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．设i为虚数单位，则复数z=$\frac{{{i^{2015}}}}{{1-{i^{2015}}}}$在复平面中对应的点在（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    同步练习册答案