
| A�� | $\frac{\sqrt{10}}{2}$ | B�� | $\frac{\sqrt{6}}{2}$ | C�� | $\frac{5}{2}$ | D�� | $\frac{3}{2}$ |
���� �����ҽ���ΪF��c��0������B��0��b�����߶�BF��˫����C����֧���ڵ�A��$\overrightarrow{BA}=2\overrightarrow{AF}$��ȷ��A�����꣬����˫���߷��̣��������˫���ߵ������ʣ�
��� �⣺��A��x��y����
���ҽ���ΪF��c��0������B��0��b�����߶�BF��˫����C����֧���ڵ�A��$\overrightarrow{BA}=2\overrightarrow{AF}$��
��x=$\frac{2c}{3}$��y=$\frac{b}{3}$��
����˫���߷��̣��ɵ�$\frac{4}{9}��\frac{{c}^{2}}{{a}^{2}}$-$\frac{1}{9}$=1
��e=$\frac{\sqrt{10}}{2}$��
��ѡ��A��
���� ���⿼������֪ʶ�����ã�����˫���ߵ������ʣ���������֪ʶȷ��A�������ǹؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3��x��4 | B�� | x��4 | C�� | 0��x��2 | D�� | 2��x��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����ֱ��y=x�Գ� | B�� | ����ԭ��Գ� | C�� | ����x��Գ� | D�� | ����y��Գ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 9 | B�� | 10 | C�� | 11 | D�� | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
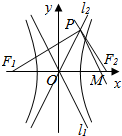 ��֪F1��F2�ֱ���˫����$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ��㣬l1��l2Ϊ˫���ߵ����������ߣ������M��b��0����ƽ����l1��ֱ�߽�l2�ڵ�P����PF1��PF2�����˫���ߵ�������Ϊ��������
��֪F1��F2�ֱ���˫����$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ��㣬l1��l2Ϊ˫���ߵ����������ߣ������M��b��0����ƽ����l1��ֱ�߽�l2�ڵ�P����PF1��PF2�����˫���ߵ�������Ϊ��������| A�� | $\sqrt{3}$ | B�� | $\sqrt{5}$ | C�� | $\frac{\sqrt{14-2\sqrt{41}}}{2}$ | D�� | $\frac{\sqrt{14+2\sqrt{41}}}{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com