
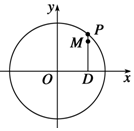
 如图,设P是圆x2+y2=6上的动点,点D是P在x轴上的投影,M为线段PD上一点,且$|{DP}|=\sqrt{2}|{DM}|$.
如图,设P是圆x2+y2=6上的动点,点D是P在x轴上的投影,M为线段PD上一点,且$|{DP}|=\sqrt{2}|{DM}|$.分析 (1)由题意P是圆x2+y2=6上的动点,点D是P在x轴上的射影,M为PD上一点,且$|{DP}|=\sqrt{2}|{DM}|$,利用相关点法即可求轨迹;
(2)联立直线方程与椭圆方程,求出|EG|,再由题意设出FH所在直线方程,与椭圆方程联立,利用弦长公式求得|FH|的最大值,代入四边形面积公式求得答案.
解答 解:(1)设M的坐标为(x,y),P的坐标为(xp,yp)
由已知$|{DP}|=\sqrt{2}|{DM}|$得:xp=x,yp=$\sqrt{2}$y,
∵P是圆x2+y2=6上的动点,
∴x2+2y2=6,即$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{3}=1$;
(2)联立$\left\{\begin{array}{l}{x+y-\sqrt{3}=0}\\{\frac{{x}^{2}}{6}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得$3{x}^{2}-4\sqrt{3}x=0$.
解得:${x}_{E}=0,{x}_{G}=\frac{4\sqrt{3}}{3}$.
∴|EG|=$\sqrt{2}|{x}_{E}-{x}_{G}|$=$\sqrt{2}×\frac{4\sqrt{3}}{3}=\frac{4\sqrt{6}}{3}$.
由题意可设F、H所在直线方程为y=x+m.
联立$\left\{\begin{array}{l}{y=x+m}\\{\frac{{x}^{2}}{6}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得3x2+4mx+2m2-6=0.
由△=16m2-12(2m2-6)=-8m2+72>0,得-3<m<3.
${x}_{F}+{x}_{H}=-\frac{4m}{3}$,${x}_{F}•{x}_{H}=\frac{2{m}^{2}-6}{3}$.
|FH|=$\sqrt{2}\sqrt{(-\frac{4m}{3})^{2}-4•\frac{2{m}^{2}-6}{3}}$=$\frac{\sqrt{2}}{3}\sqrt{72-8{m}^{2}}$.
∴当m=0时,|FH|max=4.
∴$({S}_{EFGH})_{max}=\frac{1}{2}×\frac{4\sqrt{6}}{3}×4=\frac{8\sqrt{6}}{3}$.
点评 本题考查椭圆的简单性质,考查直线与椭圆位置关系的应用,考查计算能力,属中档题.


科目:高中数学 来源: 题型:解答题
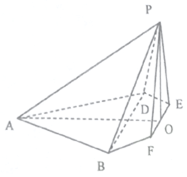 在边长为4的菱形ABCD中,∠DAB=60°,点E,F分别是边CD,CB的中点,AC∩EF=O,沿EF将△CEF翻折到△PEF,连接PA,PB,PD,得到如图的五棱锥,且$PB=\sqrt{10}$.
在边长为4的菱形ABCD中,∠DAB=60°,点E,F分别是边CD,CB的中点,AC∩EF=O,沿EF将△CEF翻折到△PEF,连接PA,PB,PD,得到如图的五棱锥,且$PB=\sqrt{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
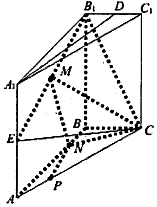 已知在三棱柱ABC-A1B1C1中,B1B⊥平面ABC,∠ABC=90°,B1B=AB=2BC=4,D、E分别是B1C1,A1A的中点.
已知在三棱柱ABC-A1B1C1中,B1B⊥平面ABC,∠ABC=90°,B1B=AB=2BC=4,D、E分别是B1C1,A1A的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a)<f(b)<f(c) | B. | f(a)<f(c)<f(b) | C. | f(b)<f(c)<f(a) | D. | f(c)<f(b)<f(a) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com