
分析 利用三角函数恒等变换的应用化简等式左边等于右边即可得证.
解答 证明:(1)左边=$\frac{1+sin2φ}{sinφ+cosφ}$=$\frac{(sinφ+cosφ)^{2}}{sinφ+cosφ}$=sinφ+cosφ=右边,得证;
(2)左边=sinθ(1+cos2θ)=sinθ(1+2cos2θ-1)=2sinθcos2θ=sin2θcosθ=右边,得证;
(3)左边=$\frac{1-ta{n}^{2}\frac{α}{2}}{1+ta{n}^{2}\frac{α}{2}}$=$\frac{\frac{co{s}^{2}\frac{α}{2}-si{n}^{2}\frac{α}{2}}{co{s}^{2}\frac{α}{2}}}{\frac{co{s}^{2}\frac{α}{2}+si{n}^{2}\frac{α}{2}}{co{s}^{2}\frac{α}{2}}}$=coaα=右边,得证;
(4)左边=4sinθcos2$\frac{θ}{2}$=4sinθ×$\frac{1+cosθ}{2}$=2sinθ+sin2θ=右边,得证;
(5)左边=$\frac{2sinα-sin2α}{2sinα+sin2α}$=$\frac{2sinα-2sinαcosα}{2sinα+2sinαcosα}$=$\frac{1-cosα}{1+cosα}$=$\frac{2si{n}^{2}\frac{α}{2}}{2co{s}^{2}\frac{α}{2}}$=tan2$\frac{α}{2}$=右边,得证;
(6)左边=cosα(cosα-cosβ)+sinα(sinα-sinβ)
=cos2α-cosαcosβ+sin2α-sinαsinβ
=1-(cosαcosβ+sinαsinβ)
=1-cos(α-β)
=2sin2$\frac{α-β}{2}$
=右边,得证.
点评 本题主要考查了三角函数恒等变换的应用,考查了转化思想,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
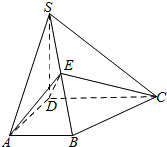 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,SD=2,E为棱SB上的一点,且SE=2EB,CE与平面SAB所成角的正弦值为$\frac{\sqrt{30}}{10}$.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,SD=2,E为棱SB上的一点,且SE=2EB,CE与平面SAB所成角的正弦值为$\frac{\sqrt{30}}{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届重庆市高三理上适应性考试一数学试卷(解析版) 题型:解答题
选修4-1:几何证明选讲
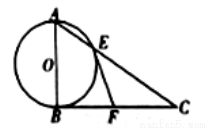
如图,在 中,
中,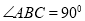 ,以
,以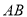 为直径的圆交
为直径的圆交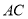 于点
于点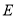 ,过点
,过点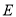 作圆
作圆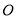 的切线交
的切线交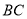 于点
于点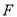 .
.
(1)求证: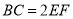 ;
;
(2)若 ,求
,求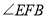 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com