练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．“x=2”是“（x-2）•（x+5）=0”的（　　）
    A．必要不充分条件B．充分不必要条件
    C．充要条件D．既不充分也不必要条件

    分析 解方程“（x-2）•（x+5）=0”，进而结合充要条件的定义可得答案．

    解答 解：当“x=2”时，“（x-2）•（x+5）=0”成立，
    故“x=2”是“（x-2）•（x+5）=0”的充分条件；
    当“（x-2）•（x+5）=0”时，“x=2”不一定成立，
    故“x=2”是“（x-2）•（x+5）=0”的不必要条件，
    故“x=2”是“（x-2）•（x+5）=0”的充分不必要条件，
    故选：B．

    点评 本题考查的知识点是充要条件，熟练掌握充要条件的概念，是解答的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    16．已知动点P到定点F（p，0）和到直线x=-p（p＞0）的距离相等．
    （Ⅰ）求动点P的轨迹C的方程；
    （Ⅱ）经过点F的直线l交（Ⅰ）中轨迹C于A、B两点，点D在抛物线的准线上，且BD∥x轴．证明直线AD经过原点O．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．若定义在R上的函数f（x），g（x）满足f（x-1）=f（1-x），g（x）=f（x-2），且f（x1）＞f（x2）＞f（1）（x1＞x2＞0），g（0）=3，g（2）=1，若g（x）在[0，m]上有最小值1，最大值3，则m的取值范围是（　　）
    A．（0，+∞）B．（0，2]C．[2，4]D．[2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．函数f（x）=logax（其中a＞0，且a≠1）的图象恒过定点（1，0）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知函数f（x）=x-$\frac{1}{x}$．
    （1）判断函数f（x）的奇偶性，并加以证明；
    （2）判断函数f（x）的单调性，并加以证明；
    （3）若函数f（x）在区间[2，a]上的最大值与最小值之和不小于$\frac{11a-2}{2a}$，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知a，b∈R，且ab≠0，那么“a＞b”是“lg（a-b）＞0”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充分必要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．函数y=（x-1）3+1的图象的中心对称点的坐标是（1，1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

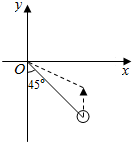    12．如图，据气象部门预报，在距离码头O南偏东45°方向600km处的热带风暴中心正以20km/h的速度向正北方向移动，距台风中心450km以内的地区都将受到影响．据以上预报估计，从现在起多长时间后，该码头将受到热带风暴的影响，影响时间大约有多长？（精确到0.1h，$\sqrt{2}≈$1.414）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．证明下列等式：
    （1）$\frac{1+sin2φ}{sinφ+cosφ}$=sinφ+cosφ
    （2）sinθ（1+cos2θ）=sin2θcosθ
    （3）$\frac{1-ta{n}^{2}\frac{α}{2}}{1+ta{n}^{2}\frac{α}{2}}$=coaα
    （4）4sinθcos2$\frac{θ}{2}$=2sinθ+sin2θ：
    （5）$\frac{2sinα-sin2α}{2sinα+sin2α}$=tan2$\frac{α}{2}$
    （6）cosα（cosα-cosβ）+sinα（sinα-sinβ）=2sin2$\frac{α-β}{2}$．

    查看答案和解析>>

    同步练习册答案