
分析 (Ⅰ)根据题意,利用抛物线定义得到动点P的轨迹C是以F为焦点,以直线x=-p(p>0)为准线的抛物线,求出动点P的轨迹C的方程即可;
(Ⅱ)设经过点F的直线l的方程可设为x=my+p,代入抛物线解析式,消去x得到关于y的一元二次方程,利用根与系数的关系表示出y1y2,由BD与x轴平行,且在抛物线准线上,设出D坐标,进而表示出$\overrightarrow{OA}$与$\overrightarrow{OD}$,利用平面向量运算法则判断出$\overrightarrow{OA}$与$\overrightarrow{OD}$共线,且有公共点,即可得证.
解答 (Ⅰ)解:∵动点P到定点F(p,0)和到直线x=-p(p>0)的距离相等,
∴由抛物线定义知,动点P的轨迹C是以F为焦点,以直线x=-p(p>0)为准线的抛物线,
则轨迹C的方程是y2=4px;
(Ⅱ)证明:经过点F的直线l的方程可设为x=my+p,
代入抛物线方程得:y2-4pmy-4p2=0,
若记A(x1,y1),B(x2,y2),
则y1,y2是该方程的两个根,
∴y1y2=-4p2,
∵BD∥x轴,且点D在准线x=-p上,
∴点D的坐标为(-p,y2),
∴$\overrightarrow{OA}$=(x1,y1),$\overrightarrow{OD}$=(-p,y2),
∵x1y2+py1=$\frac{{{y}_{1}}^{2}{y}_{2}}{4p}$+py1=$\frac{-4{p}^{2}{y}_{1}}{4p}$+py1=-py1+py1=0,
∴向量$\overrightarrow{OA}$,$\overrightarrow{OD}$共线,且$\overrightarrow{OA}$,$\overrightarrow{OD}$有共同的起点O,
则直线AC经过原点O.
点评 此题考查了抛物线的简单性质,抛物线的定义,以及平面向量的数量积运算法则,熟练掌握抛物线的定义是解本题的关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
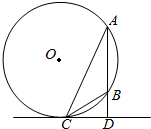 如图,A、B是圆O上的两点,且AB的长度小于圆O的直径,直线l与AB垂于点D且与圆O相切于点C.若AB=2,DB=1
如图,A、B是圆O上的两点,且AB的长度小于圆O的直径,直线l与AB垂于点D且与圆O相切于点C.若AB=2,DB=1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
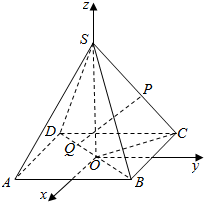 在正四棱锥S-ABCD中,底面边长为a,侧棱长也为a,以底面中心O为坐标原点,建立如图所示的空间直角坐标系,P点在侧棱SC上,Q点在底面ABCD的对角线BD上,试求P、Q两点间的最小距离.
在正四棱锥S-ABCD中,底面边长为a,侧棱长也为a,以底面中心O为坐标原点,建立如图所示的空间直角坐标系,P点在侧棱SC上,Q点在底面ABCD的对角线BD上,试求P、Q两点间的最小距离.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4件都是正品 | B. | 至少有一件次品 | C. | 4件都是次品 | D. | 至少有一件正品 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{4-π}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
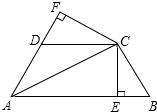 如图,已知AC平分∠BAD,CE⊥AB于点E,CF⊥AD于点F,且BC=CD.
如图,已知AC平分∠BAD,CE⊥AB于点E,CF⊥AD于点F,且BC=CD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com