
【题目】已知命题![]() 函数
函数![]() 是
是![]() 上的奇函数,命题
上的奇函数,命题![]() 函数
函数![]() 的定义域和值域都是
的定义域和值域都是![]() ,其中
,其中![]() .
.
(1)若命题![]() 为真命题,求实数
为真命题,求实数![]() 的值;
的值;
(2)若“![]() 且
且![]() ”为假命题,“
”为假命题,“![]() 或
或![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】分析:(1)根据奇函数定义得f(-x)+f(x)=0,解得实数![]() 的值;(2)根据函数
的值;(2)根据函数![]() 单调性得
单调性得![]() 转化为对应一元二次方程有两个大于1的不相等实根,利用实根分布解得k的取值范围,由“p且q”为假命题,“p或q”为真命题,得命题p和q中有且仅有一个为真命题,根据真假列方程组解得实数
转化为对应一元二次方程有两个大于1的不相等实根,利用实根分布解得k的取值范围,由“p且q”为假命题,“p或q”为真命题,得命题p和q中有且仅有一个为真命题,根据真假列方程组解得实数![]() 的取值范围.
的取值范围.
详解:(1)若命题p为真命题,则f(-x)+f(x)=0,
即![]() ,
,
化简得![]() 对任意的x∈R成立,
对任意的x∈R成立,
所以k=1.
(2)若命题q为真命题,因为![]() 在[a,b]上恒成立,
在[a,b]上恒成立,
所以g(x)在[a,b]上是单调增函数,
又g(x)的定义域和值域都是[a,b],所以![]()
所以a,b是方程![]() 的两个不相等的实根,且1<a<b.
的两个不相等的实根,且1<a<b.
即方程![]() 有两个大于1的实根且不相等,
有两个大于1的实根且不相等,
记h(x)=k2x2-k(2k-1)x+1,
故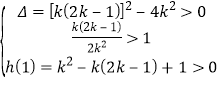 ,解得
,解得![]() ,
,
所以k的取值范围为![]() .
.
因为“p且q”为假命题,“p或q”为真命题,
所以命题p和q中有且仅有一个为真命题,
即p真q假,或p假q真.
所以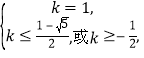 或
或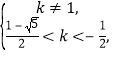
所以实数k的取值范围为![]() .
.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】将圆的一组![]() 等分点分别涂上红色或蓝色,从任意一点开始,按逆时针方向依次记录
等分点分别涂上红色或蓝色,从任意一点开始,按逆时针方向依次记录![]() 个点的颜色,称为该圆的一个“
个点的颜色,称为该圆的一个“![]() 阶色序”,当且仅当两个“
阶色序”,当且仅当两个“![]() 阶色序”对应位置上的颜色至少有一个不相同时,称为不同的“
阶色序”对应位置上的颜色至少有一个不相同时,称为不同的“![]() 阶色序”.若某圆的任意两个“
阶色序”.若某圆的任意两个“![]() 阶色序”均不相同,则称该圆为“
阶色序”均不相同,则称该圆为“![]() 阶魅力圆”.“4阶魅力圆”中最多可有的等分点个数为__________.
阶魅力圆”.“4阶魅力圆”中最多可有的等分点个数为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 平面上,将两个半圆弧
平面上,将两个半圆弧![]() 和
和![]() 、两条直线
、两条直线![]() 和
和![]() 围成的封闭图形记为
围成的封闭图形记为![]() ,如图中阴影部分.记
,如图中阴影部分.记![]() 绕
绕![]() 轴旋转一周而成的几何体为
轴旋转一周而成的几何体为![]() ,过
,过![]() 作
作![]() 的水平截面,所得截面面积为
的水平截面,所得截面面积为![]() ,试利用祖暅原理(祖暅原理:“幂势既同,则积不容异”,意思是:两等高的几何体在同高处被截得的两个截面面积均相等,那么这两个几何体的体积相等)、一个平放的圆柱和一个长方体,得出
,试利用祖暅原理(祖暅原理:“幂势既同,则积不容异”,意思是:两等高的几何体在同高处被截得的两个截面面积均相等,那么这两个几何体的体积相等)、一个平放的圆柱和一个长方体,得出![]() 的体积值为__________.
的体积值为__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}前n项和Sn满足:2Sn+an=1.
(1)求数列{an}的通项公式;
(2)设 ![]() ,数列{bn}的前n项和为Tn , 求证:Tn<2.
,数列{bn}的前n项和为Tn , 求证:Tn<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1 , F2为双曲线C: ![]() 的左,右焦点,P,Q为双曲线C右支上的两点,若
的左,右焦点,P,Q为双曲线C右支上的两点,若 ![]() =2
=2 ![]() ,且
,且 ![]()
![]() =0,则该双曲线的离心率是( )
=0,则该双曲线的离心率是( )
A.![]()
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果数列![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() ,且
,且![]() ),满足:①
),满足:①![]() ,
,![]() ;
;
②![]() ,那么称数列
,那么称数列![]() 为“
为“![]() ”数列.
”数列.
(![]() )已知数列
)已知数列![]() ,
,![]() ,
,![]() ,
,![]() ;数列
;数列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .试判断数列
.试判断数列![]() ,
,![]() 是否为“
是否为“![]() ”数列.
”数列.
(![]() )是否存在一个等差数列是“
)是否存在一个等差数列是“![]() ”数列?请证明你的结论.
”数列?请证明你的结论.
(![]() )如果数列
)如果数列![]() 是“
是“![]() ”数列,求证:数列
”数列,求证:数列![]() 中必定存在若干项之和为
中必定存在若干项之和为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com