【题目】设F1 ， F2为双曲线C： 
的左，右焦点，P，Q为双曲线C右支上的两点，若 
=2 
，且 
=0，则该双曲线的离心率是（ ）
A.
B.2
C.
D.
【答案】C
【解析】解：∵经过右焦点F2的直线与双曲线C的右支交于P，Q两点，且|PF2|=2|F2Q|， ∴设|F2Q|=m，则|PF2|=2|F2Q|=2m，
|PF1|=|PF2|+2a=2m+2a，
|QF1|=|QF2|+2a=m+2a，
∵PQ⊥F1Q，
∴|PF1|2=|PQ|2+|QF1|2 ，
即（2m+2a）2=（3m）2+（m+2a）2 ，
整理得4m2+8ma+4a2=9m2+m2+8ma+4a2 ，
即4am=6m2 ，
则m= 
a，
则|QF1|= a+2a= 
，|F2Q|= a，
由|F1F2|2=|F1Q|2+|QF2|2 ，
即4c2=（ ）2+（ a）2= 
，
则e= 
= 
，
故选：C．
科目：高中数学 来源： 题型：
【题目】如图，甲、乙两个企业的用电负荷量
关于投产持续时间
（单位：小时）的关系
均近似地满足函数
．
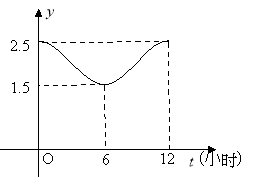
（1）根据图象，求函数
的解析式；
（2）为使任意时刻两企业用电负荷量之和不超过
，现采用错峰用电的方式，让企业乙比企业甲推迟
小时投产，求的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知命题
函数
是
上的奇函数，命题
函数
的定义域和值域都是
，其中
.
（1）若命题
为真命题，求实数
的值；
（2）若“且
”为假命题，“或”为真命题，求实数的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
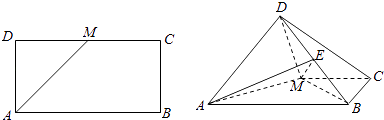
【题目】如图，已知长方形ABCD中，AB=2 
，AD= ，M为DC的中点，将△ADM沿AM折起，使得平面ADM⊥平面ABCM （Ⅰ）求证：AD⊥BM
（Ⅱ）若点E是线段DB上的一动点，问点E在何位置时，二面角E﹣AM﹣D的余弦值为 
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）= 
，方程f2（x）+mf（x）=0（m∈R）有四个不相等的实数根，则实数m的取值范围是（ ）
A.（﹣∞，﹣ 
）
B.（﹣ ，0）
C.（﹣ ，+∞）
D.（0， ）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】双曲线
的虚轴长为
，两条渐近线方程为
.
（1）求双曲线
的方程；
（2）双曲线上有两个点
，直线
和
的斜率之积为，判别
是否为定值，；
（3）经过点
的直线
且与双曲线有两个交点
，直线的倾斜角是
，是否存在直线
（其中
）使得
恒成立？（其中
分别是点到
的距离）若存在，求出
的值，若不存在，请说明理由.
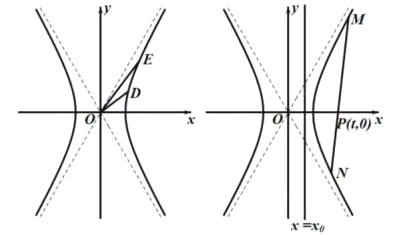
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某商场举行有奖促销活动，顾客购买一定金额的商品后即可参加一次抽奖.随着抽奖活动的有效开展，参与抽奖活动的人数越来越多，该商场对前5天抽奖活动的人数进行统计，y表示第x天参加抽奖活动的人数，得到统计表如下：
x | 1 | 2 | 3 | 4 | 5 |
y | 50 | 60 | 70 | 80 | 100 |
经过进一步统计分析，发现y与x具有线性相关关系.
（1）若从这5天随机抽取两天，求至少有1天参加抽奖人数超过70的概率；
（2）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程
，并估计该活动持续7天，共有多少名顾客参加抽奖？
参考公式及数据：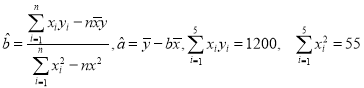
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】数列{an}的前n项和是Sn ， 且Sn+ 
an=1，数列{bn}，{cn}满足bn=log3 
，cn= 
． （Ⅰ）求数列{an}的通项公式；
（Ⅱ）数列{cn}的前n项和为Tn ， 若不等式Tn＜m对任意的正整数n恒成立，求m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知等差数列{an}的前n项和为Sn ， 且满足S4=24，S7=63． （Ⅰ）求数列{an}的通项公式；
（Ⅱ）若 
，求数列{bn}的前n项和Tn ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com