
【题目】如图,甲、乙两个企业的用电负荷量![]() 关于投产持续时间
关于投产持续时间![]() (单位:小时)的关系
(单位:小时)的关系![]() 均近似地满足函数
均近似地满足函数![]()
![]() .
.
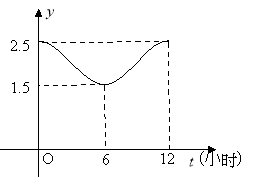
(1)根据图象,求函数![]() 的解析式;
的解析式;
(2)为使任意时刻两企业用电负荷量之和不超过![]() ,现采用错峰用电的方式,让企业乙比企业甲推迟
,现采用错峰用电的方式,让企业乙比企业甲推迟![]()
![]() 小时投产,求
小时投产,求![]() 的最小值.
的最小值.
【答案】(1)![]() (2)4
(2)4
【解析】
试题(1)由图象可得:![]() ,周期
,周期![]() ,
,![]() ,求得
,求得![]() 的解析式;(2)设乙投产持续时间为
的解析式;(2)设乙投产持续时间为![]() 小时,则甲的投产持续时间为(
小时,则甲的投产持续时间为(![]() )小时,企业乙用电负荷量随持续时间
)小时,企业乙用电负荷量随持续时间![]() 变化的关系式为:
变化的关系式为:![]() ;同理,企业甲用电负荷量变化关系式为:
;同理,企业甲用电负荷量变化关系式为:![]() ; 两企业用电负荷量之和为
; 两企业用电负荷量之和为![]() ,依题意,有
,依题意,有![]() 恒成立,求得m最值 ;
恒成立,求得m最值 ;
试题解析:(Ⅰ)由图象可得:![]() ,
,
解得![]()
周期![]() ,
,![]() ,
,
![]() ,
,
又![]()
![]() 过点
过点![]() ,
,
![]() 且
且![]() ,
,![]() ,
,
![]()
(Ⅱ)设乙投产持续时间为![]() 小时,则甲的投产持续时间为(
小时,则甲的投产持续时间为(![]() )小时
)小时
由诱导公式,企业乙用电负荷量随持续时间![]() 变化的关系式为:
变化的关系式为:![]() ;
;
同理,企业甲用电负荷量变化关系式为:![]() ;
;
两企业用电负荷量之和
![]() ;
;
依题意,有![]() 恒成立,
恒成立,
即![]() 恒成立,
恒成立,
展开有:![]() 恒成立,------10分
恒成立,------10分
![]()
(其 );
);
![]() ,
,
整理得到:![]() ,
,
依据余弦函数图像得:![]() ,
,
即![]() ,取
,取![]() 得:
得:![]()
∴![]() 的最小值为4.
的最小值为4.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
【题目】已知a>0,b>0,函数f(x)=|x+a|+|2x﹣b|的最小值为1.
(1)求证:2a+b=2;
(2)若a+2b≥tab恒成立,求实数t的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ).
).
(1)若曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 平行,求
平行,求![]() 的值;
的值;
(2)若对于任意![]() 且
且![]() ,都有
,都有![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
(3)若对于任意![]() ,都有
,都有![]() 成立,求整数
成立,求整数![]() 的最大值.
的最大值.
(其中![]() 为自然对数的底数)
为自然对数的底数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() ,圆Q:x2+y2﹣4x﹣2y+3=0的圆心Q在椭圆C上,点P(0,1)到椭圆C的右焦点的距离为2.
,圆Q:x2+y2﹣4x﹣2y+3=0的圆心Q在椭圆C上,点P(0,1)到椭圆C的右焦点的距离为2. 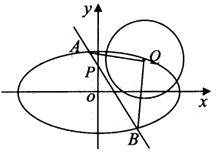
(1)求椭圆C的方程;
(2)过点P作直线l交椭圆C于A,B两点,若S△AQB=tan∠AQB,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂家具车间造![]() 、
、![]() 型两类桌子,每张桌子需木工和漆工梁道工序完成.已知木工做一张
型两类桌子,每张桌子需木工和漆工梁道工序完成.已知木工做一张![]() 、
、![]() 型型桌子分别需要1小时和2小时,漆工油漆一张
型型桌子分别需要1小时和2小时,漆工油漆一张![]() 、
、![]() 型型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张
型型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张![]() 、
、![]() 型型桌子分别获利润2千元和3千元.
型型桌子分别获利润2千元和3千元.
(1)列出满足生产条件的数学关系式,并画出可行域;
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆的一组![]() 等分点分别涂上红色或蓝色,从任意一点开始,按逆时针方向依次记录
等分点分别涂上红色或蓝色,从任意一点开始,按逆时针方向依次记录![]() 个点的颜色,称为该圆的一个“
个点的颜色,称为该圆的一个“![]() 阶色序”,当且仅当两个“
阶色序”,当且仅当两个“![]() 阶色序”对应位置上的颜色至少有一个不相同时,称为不同的“
阶色序”对应位置上的颜色至少有一个不相同时,称为不同的“![]() 阶色序”.若某圆的任意两个“
阶色序”.若某圆的任意两个“![]() 阶色序”均不相同,则称该圆为“
阶色序”均不相同,则称该圆为“![]() 阶魅力圆”.“4阶魅力圆”中最多可有的等分点个数为__________.
阶魅力圆”.“4阶魅力圆”中最多可有的等分点个数为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1 , F2为双曲线C: ![]() 的左,右焦点,P,Q为双曲线C右支上的两点,若
的左,右焦点,P,Q为双曲线C右支上的两点,若 ![]() =2
=2 ![]() ,且
,且 ![]()
![]() =0,则该双曲线的离心率是( )
=0,则该双曲线的离心率是( )
A.![]()
B.2
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com