
【题目】已知函数![]() (
(![]() ).
).
(1)若曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 平行,求
平行,求![]() 的值;
的值;
(2)若对于任意![]() 且
且![]() ,都有
,都有![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
(3)若对于任意![]() ,都有
,都有![]() 成立,求整数
成立,求整数![]() 的最大值.
的最大值.
(其中![]() 为自然对数的底数)
为自然对数的底数)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】分析:(1)由题意得:![]() ,由题意可得
,由题意可得![]() ,解得
,解得![]() .
.
(2)因为![]() ,所以
,所以![]() ,
,
记![]() ,可知
,可知![]() 在
在![]() 上单调递增.
上单调递增.
所以![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,记
上恒成立,记![]() ,即可求得
,即可求得![]() 的取值范围.
的取值范围.
(3)若对于任意![]() ,都有
,都有![]() 成立,
成立,
所以![]() 对于任意
对于任意![]() 恒成立,
恒成立,
即![]() 对于任意
对于任意![]() 恒成立,
恒成立,
令![]() ,利用导数研究函数
,利用导数研究函数![]() 的性质,即可得到整数
的性质,即可得到整数![]() 的最大值.
的最大值.
详解:
(1)由题意得:![]() ,
,
又曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 平行,
平行,
所以![]() ,解得
,解得![]() .
.
(2)因为![]() ,所以
,所以![]() ,
,
记![]() ,又因为
,又因为![]() 且
且![]() ,
,
所以![]() 在
在![]() 上单调递增.
上单调递增.
所以![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,记
上恒成立,记![]() ,
,
所以![]() ,令
,令![]() ,解得
,解得![]() ,
,
因为当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
所以当![]() 时,
时,![]() 取到最大值
取到最大值![]() ,
,
所以![]() .
.
(3)若对于任意![]() ,都有
,都有![]() 成立,
成立,
所以![]() 对于任意
对于任意![]() 恒成立,
恒成立,
即![]() 对于任意
对于任意![]() 恒成立,
恒成立,
令![]() ,所以
,所以![]() ,
,
再令![]() ,所以
,所以![]() 在
在![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,
,![]() ,
,
所以必存在唯一的解![]() ,使得
,使得![]() ,
,
即![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
所以 ,
,
因为![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() 的最大整数为
的最大整数为![]() ,
,
所以整数![]() 的最大值为
的最大值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆C的参数方程为 ![]() (θ为参数),以O为极点,x轴的非负半轴为极轴且取相同的单位长度建立极坐标系.
(θ为参数),以O为极点,x轴的非负半轴为极轴且取相同的单位长度建立极坐标系.
(1)求圆C的极坐标方程;
(2)若直线l的极坐标方程是 ![]() ,射线
,射线 ![]() 与圆C的交点为O、P,与直线l的交点为Q.求线段PQ的长.
与圆C的交点为O、P,与直线l的交点为Q.求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某项“过关游戏”规则规定:在地![]() 关要抛掷
关要抛掷![]() 颗骰子
颗骰子![]() 次,如果这
次,如果这![]() 次抛掷所出现的点数和大于
次抛掷所出现的点数和大于![]() ,则算过关.
,则算过关.
(Ⅰ)此游戏最多能过__________关.
(Ⅱ)连续通过第![]() 关、第
关、第![]() 关的概率是__________.
关的概率是__________.
(Ⅲ)若直接挑战第![]() 关,则通关的概率是__________.
关,则通关的概率是__________.
(Ⅳ)若直接挑战第![]() 关,则通关的概率是__________.
关,则通关的概率是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (
( ![]() ),若函数F(x)=f(x)﹣3的所有零点依次记为x1 , x2 , x3 , …,xn , 且x1<x2<x3<…<xn , 则x1+2x2+2x3+…+2xn﹣1+xn= .
),若函数F(x)=f(x)﹣3的所有零点依次记为x1 , x2 , x3 , …,xn , 且x1<x2<x3<…<xn , 则x1+2x2+2x3+…+2xn﹣1+xn= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
|
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图:
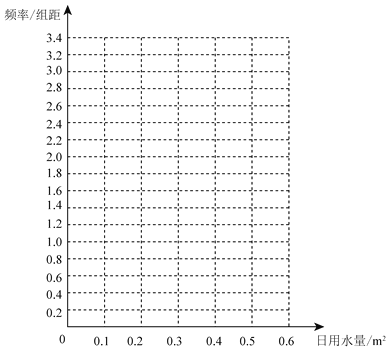
(2)估计该家庭使用节水龙头后,日用水量小于0.35 m3的概率;
(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,甲、乙两个企业的用电负荷量![]() 关于投产持续时间
关于投产持续时间![]() (单位:小时)的关系
(单位:小时)的关系![]() 均近似地满足函数
均近似地满足函数![]()
![]() .
.
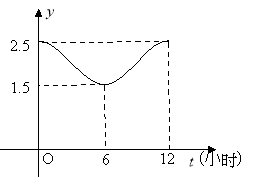
(1)根据图象,求函数![]() 的解析式;
的解析式;
(2)为使任意时刻两企业用电负荷量之和不超过![]() ,现采用错峰用电的方式,让企业乙比企业甲推迟
,现采用错峰用电的方式,让企业乙比企业甲推迟![]()
![]() 小时投产,求
小时投产,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
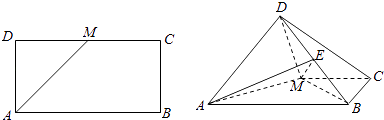
【题目】如图,已知长方形ABCD中,AB=2 ![]() ,AD=
,AD= ![]() ,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM (Ⅰ)求证:AD⊥BM
,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM (Ⅰ)求证:AD⊥BM
(Ⅱ)若点E是线段DB上的一动点,问点E在何位置时,二面角E﹣AM﹣D的余弦值为 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com