
【题目】已知函数f(x)= ![]() ,方程f2(x)+mf(x)=0(m∈R)有四个不相等的实数根,则实数m的取值范围是( )
,方程f2(x)+mf(x)=0(m∈R)有四个不相等的实数根,则实数m的取值范围是( )
A.(﹣∞,﹣ ![]() )
)
B.(﹣ ![]() ,0)
,0)
C.(﹣ ![]() ,+∞)
,+∞)
D.(0, ![]() )
)
【答案】B
【解析】解:当x<0时,f(x)=﹣xex , 则f′(x)=﹣(x+1)ex ,
由f′(x)=0得x=﹣1,
当x<﹣1时,f′(x)>0,
当﹣1<x<0时,f′(x)<0,
即当x=﹣1时,函数f(x)取得极大值,此时f(﹣1)= ![]() ,
,
且当x<0时,f(x)>0,
当x≥0时,f(x)=ln(x+1)≥0,
设t=f(x),
则当t= ![]() 时,方程t=f(x)有两个根,
时,方程t=f(x)有两个根,
当t> ![]() 或t=0时,方程t=f(x)有1个根,
或t=0时,方程t=f(x)有1个根,
当0<t< ![]() 时,方程t=f(x)有3个根,
时,方程t=f(x)有3个根,
当t<0时,方程t=f(x)有0个根,
则方程f2(x)+mf(x)=0(m∈R)等价为t2+mt=0,
即t=0或t=﹣m,
当t=0时,方程t=f(x)有1个根,
∴若方程f2(x)+mf(x)=0(m∈R)有四个不相等的实数根,
则等价为t=f(x)有3个根,
即0<﹣m< ![]() ,得﹣
,得﹣ ![]() <m<0,
<m<0,
故选:B.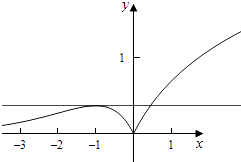


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() ,圆Q:x2+y2﹣4x﹣2y+3=0的圆心Q在椭圆C上,点P(0,1)到椭圆C的右焦点的距离为2.
,圆Q:x2+y2﹣4x﹣2y+3=0的圆心Q在椭圆C上,点P(0,1)到椭圆C的右焦点的距离为2. 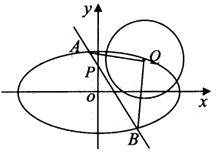
(1)求椭圆C的方程;
(2)过点P作直线l交椭圆C于A,B两点,若S△AQB=tan∠AQB,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 平面上,将两个半圆弧
平面上,将两个半圆弧![]() 和
和![]() 、两条直线
、两条直线![]() 和
和![]() 围成的封闭图形记为
围成的封闭图形记为![]() ,如图中阴影部分.记
,如图中阴影部分.记![]() 绕
绕![]() 轴旋转一周而成的几何体为
轴旋转一周而成的几何体为![]() ,过
,过![]() 作
作![]() 的水平截面,所得截面面积为
的水平截面,所得截面面积为![]() ,试利用祖暅原理(祖暅原理:“幂势既同,则积不容异”,意思是:两等高的几何体在同高处被截得的两个截面面积均相等,那么这两个几何体的体积相等)、一个平放的圆柱和一个长方体,得出
,试利用祖暅原理(祖暅原理:“幂势既同,则积不容异”,意思是:两等高的几何体在同高处被截得的两个截面面积均相等,那么这两个几何体的体积相等)、一个平放的圆柱和一个长方体,得出![]() 的体积值为__________.
的体积值为__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}前n项和Sn满足:2Sn+an=1.
(1)求数列{an}的通项公式;
(2)设 ![]() ,数列{bn}的前n项和为Tn , 求证:Tn<2.
,数列{bn}的前n项和为Tn , 求证:Tn<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]()
(1)当a=1时,求函数f(x)在x=e﹣1处的切线方程;
(2)当 ![]() 时,讨论函数f(x)的单调性;
时,讨论函数f(x)的单调性;
(3)若x>0,求函数 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1 , F2为双曲线C: ![]() 的左,右焦点,P,Q为双曲线C右支上的两点,若
的左,右焦点,P,Q为双曲线C右支上的两点,若 ![]() =2
=2 ![]() ,且
,且 ![]()
![]() =0,则该双曲线的离心率是( )
=0,则该双曲线的离心率是( )
A.![]()
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究“晚上喝绿茶与失眠”有无关系,调查了100名人士,得到下面的列联表:
失眠 | 不失眠 | 合计 | |
晚上喝绿茶 | 16 | 40 | 56 |
晚上不喝绿茶 | 5 | 39 | 44 |
合计 | 21 | 79 | 100 |
由已知数据可以求得:![]() ,则根据下面临界值表:
,则根据下面临界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
可以做出的结论是( )
A. 在犯错误的概率不超过0.01的前提下认为“晚上喝绿茶与失眠有关”
B. 在犯错误的概率不超过0.01的前提下认为“晚上喝绿茶与失眠无关”
C. 在犯错误的概率不超过0.05的前提下认为“晚上喝绿茶与失眠有关”
D. 在犯错误的概率不超过0.05的前提下认为“晚上喝绿茶与失眠无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自2016年1月1日起,我国全面二孩政策正式实施,这次人口与生育政策的历史性调整,使得“要不要再生一个”“生二孩能休多久产假”等成为千千万万个家庭在生育决策上避不开的话题.为了解针对产假的不同安排方案形成的生育意愿,某调查机构随机抽取了200户有生育二胎能力的适龄家庭进行问卷调查,得到如下数据:
产假安排(单位:周) | 14 | 15 | 16 | 17 | 18 |
有生育意愿家庭数 | 4 | 8 | 16 | 20 | 26 |
(1)若用表中数据所得的频率代替概率,面对产假为14周与16周,估计某家庭有生育意愿的概率分别为多少?
(2)假设从5种不同安排方案中,随机抽取2种不同安排分别作为备选方案,然后由单位根据单位情况自主选择. ①求两种安排方案休假周数和不低于32周的概率;
②如果用ξ表示两种方案休假周数和.求随机变量ξ的分布及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 且
且![]() ,设命题
,设命题![]() :函数
:函数![]() 在
在![]() 上单调递减,命题
上单调递减,命题![]() :对任意实数
:对任意实数![]() ,不等式
,不等式![]() 恒成立.
恒成立.
(1)写出命题![]() 的否定,并求非
的否定,并求非![]() 为真时,实数
为真时,实数![]() 的取值范围;
的取值范围;
(2)如果命题“![]() ”为真命题,且“
”为真命题,且“![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com