【题目】已知数列{an}前n项和Sn满足：2Sn+an=1．
（1）求数列{an}的通项公式；
（2）设 
，数列{bn}的前n项和为Tn ， 求证：Tn＜2．
【答案】
（1）解：2Sn+an=1，2Sn+1+an+1=1，
∴2an+1+an+1=an，
∴3an+1=an，
又2S1+a1=1，
∴a1= 
，
∴{an}是以 为首项，以 为公比的等比数列，
∴an=（ ）n
（2）解：证明： 
= 
= 
=2（ 
﹣ 
）
∴Tn=2[（1﹣ 
）+（ ﹣ ）+…+（ ﹣ ）]=2（1﹣ ）＜2
【解析】（1）根据数列的递推公式和对数的运算性质即可求出数列{an}的通项公式，（2）利用裂项求和即可求出数列{bn}的前n项和Tn ， 再放缩证明即可．
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系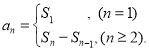
；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式才能正确解答此题．
科目：高中数学 来源： 题型：
【题目】已知函数 
（ 
），若函数F（x）=f（x）﹣3的所有零点依次记为x1 ， x2 ， x3 ， …，xn ， 且x1＜x2＜x3＜…＜xn ， 则x1+2x2+2x3+…+2xn﹣1+xn= ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=ax2﹣x﹣lnx，a∈R．
（1）当 
时，求函数f（x）的最小值；
（2）若﹣1≤a≤0，证明：函数f（x）有且只有一个零点；
（3）若函数f（x）有两个零点，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知命题
函数
是
上的奇函数，命题
函数
的定义域和值域都是
，其中
.
（1）若命题
为真命题，求实数
的值；
（2）若“且
”为假命题，“或”为真命题，求实数的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列
的首项为1，且
，数列
满足
，
，对任意
，都有
.
（1）求数列、的通项公式；
（2）令
，数列的前
项和为
.若对任意的，不等式
恒成立，试求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
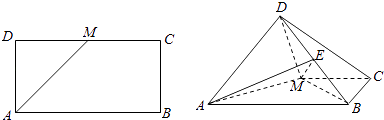
【题目】如图，已知长方形ABCD中，AB=2 
，AD= ，M为DC的中点，将△ADM沿AM折起，使得平面ADM⊥平面ABCM （Ⅰ）求证：AD⊥BM
（Ⅱ）若点E是线段DB上的一动点，问点E在何位置时，二面角E﹣AM﹣D的余弦值为 
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）= 
，方程f2（x）+mf（x）=0（m∈R）有四个不相等的实数根，则实数m的取值范围是（ ）
A.（﹣∞，﹣ 
）
B.（﹣ ，0）
C.（﹣ ，+∞）
D.（0， ）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某商场举行有奖促销活动，顾客购买一定金额的商品后即可参加一次抽奖.随着抽奖活动的有效开展，参与抽奖活动的人数越来越多，该商场对前5天抽奖活动的人数进行统计，y表示第x天参加抽奖活动的人数，得到统计表如下：
x | 1 | 2 | 3 | 4 | 5 |
y | 50 | 60 | 70 | 80 | 100 |
经过进一步统计分析，发现y与x具有线性相关关系.
（1）若从这5天随机抽取两天，求至少有1天参加抽奖人数超过70的概率；
（2）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程
，并估计该活动持续7天，共有多少名顾客参加抽奖？
参考公式及数据：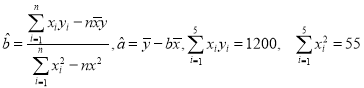
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=alnx+ 
x2﹣ax（a为常数）有两个极值点．
（1）求实数a的取值范围；
（2）设f（x）的两个极值点分别为x1 ， x2 ， 若不等式f（x1）+f（x2）＜λ（x1+x2）恒成立，求λ的最小值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com