
【题目】某部门在同一上班高峰时段对甲、乙两地铁站各随机抽取了50名乘客,统计其乘车等待时间(指乘客从进站口到乘上车的时间,乘车等待时间不超过40分钟).将统计数据按![]() 分组,制成频率分布直方图:
分组,制成频率分布直方图:
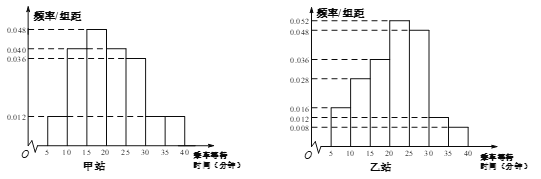
假设乘客乘车等待时间相互独立.
(1)在上班高峰时段,从甲站的乘客中随机抽取1人,记为![]() ;从乙站的乘客中随机抽取1人,记为
;从乙站的乘客中随机抽取1人,记为![]() .用频率估计概率,求“乘客
.用频率估计概率,求“乘客![]() ,
,![]() 乘车等待时间都小于20分钟”的概率;
乘车等待时间都小于20分钟”的概率;
(2)从上班高峰时段,从乙站乘车的乘客中随机抽取3人,![]() 表示乘车等待时间小于20分钟的人数,用频率估计概率,求随机变量
表示乘车等待时间小于20分钟的人数,用频率估计概率,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
【答案】(Ⅰ)![]() ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
【解析】
(I)根据频率分布直方图分别计算出两个乘客等待时间小于![]() 分钟的频率,按照相互独立事件概率计算公式,计算出“乘客
分钟的频率,按照相互独立事件概率计算公式,计算出“乘客![]() ,
,![]() 乘车等待时间都小于20分钟”的概率.(II)根据二项分布概率计算公式以及数学期望计算公式,求得
乘车等待时间都小于20分钟”的概率.(II)根据二项分布概率计算公式以及数学期望计算公式,求得![]() 的分布列和数学期望.
的分布列和数学期望.
解:(Ⅰ)设![]() 表示事件“乘客
表示事件“乘客![]() 乘车等待时间小于20分钟”,
乘车等待时间小于20分钟”,![]() 表示事件“乘客
表示事件“乘客![]() 乘车等待时间小于20分钟”,
乘车等待时间小于20分钟”,![]() 表示事件“乘客
表示事件“乘客![]() 乘车等待时间都小于20分钟”.
乘车等待时间都小于20分钟”.
由题意知,乘客![]() 乘车等待时间小于20分钟的频率为
乘车等待时间小于20分钟的频率为
![]() ,故
,故![]() 的估计值为
的估计值为![]() .
.
乘客![]() 乘车等待时间小于20分钟的频率为
乘车等待时间小于20分钟的频率为
![]() ,故
,故![]() 的估计值为
的估计值为![]() .
.
又![]() .
.
故事件![]() 的概率为
的概率为![]() .
.
(Ⅱ)由(Ⅰ)可知,乙站乘客乘车等待时间小于20分钟的频率为![]() ,
,
所以乙站乘客乘车等待时间小于20分钟的概率为![]() .
.
显然,![]() 的可能取值为
的可能取值为![]() 且
且![]() .
.
所以![]() ;
;![]() ;
;
![]() ;
;![]() .
.
故随机变量![]() 的分布列为
的分布列为
| 0 |
|
|
|
|
|
|
|
|
![]()


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:
【题目】有关命题的说法错误的是( )
A.若p∨q为假命题,则p、q均为假命题
B.“x=1”是“x2﹣3x+2=0”的充分不必要条件
C.命题“若x2﹣3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2﹣3x+2≠0”
D.对于命题p:x≥0,2x=3,则¬P:x<0,2x≠3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,平面
中,平面![]() 平面
平面![]() .四边形
.四边形![]() 为正方形,四边形
为正方形,四边形![]() 为梯形,且
为梯形,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
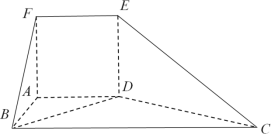
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 平面
平面![]() 若存在,求
若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现要完成下列3项抽样调查:①从20罐奶粉中抽取4罐进行食品安全卫生检查;②从某社区100户高收入家庭,270户中等收入家庭,80户低收入家庭中选出45户进行消费水平调查;③某中学报告厅有28排,每排有35个座位,一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请28名听众进行座谈.较为合理的抽样方法是( )
A.①系统抽样;②简单随机抽样;③分层抽样
B.①简单随机抽样;②分层抽样;③系统抽样
C.①分层抽样;②系统抽样;③简单随机抽样
D.①简单随机抽样;②系统抽样;③分层抽样
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com