
【题目】现要完成下列3项抽样调查:①从20罐奶粉中抽取4罐进行食品安全卫生检查;②从某社区100户高收入家庭,270户中等收入家庭,80户低收入家庭中选出45户进行消费水平调查;③某中学报告厅有28排,每排有35个座位,一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请28名听众进行座谈.较为合理的抽样方法是( )
A.①系统抽样;②简单随机抽样;③分层抽样
B.①简单随机抽样;②分层抽样;③系统抽样
C.①分层抽样;②系统抽样;③简单随机抽样
D.①简单随机抽样;②系统抽样;③分层抽样
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
【题目】某部门在同一上班高峰时段对甲、乙两地铁站各随机抽取了50名乘客,统计其乘车等待时间(指乘客从进站口到乘上车的时间,乘车等待时间不超过40分钟).将统计数据按![]() 分组,制成频率分布直方图:
分组,制成频率分布直方图:
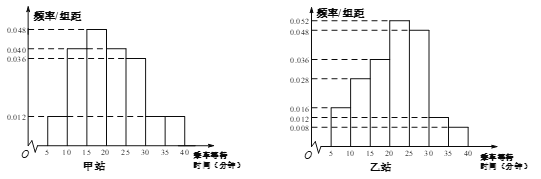
假设乘客乘车等待时间相互独立.
(1)在上班高峰时段,从甲站的乘客中随机抽取1人,记为![]() ;从乙站的乘客中随机抽取1人,记为
;从乙站的乘客中随机抽取1人,记为![]() .用频率估计概率,求“乘客
.用频率估计概率,求“乘客![]() ,
,![]() 乘车等待时间都小于20分钟”的概率;
乘车等待时间都小于20分钟”的概率;
(2)从上班高峰时段,从乙站乘车的乘客中随机抽取3人,![]() 表示乘车等待时间小于20分钟的人数,用频率估计概率,求随机变量
表示乘车等待时间小于20分钟的人数,用频率估计概率,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点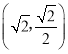 .
.
(1)求椭圆![]() 的方程;
的方程;
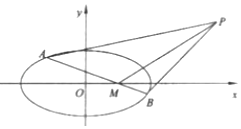
(2)设点![]() ,点
,点![]() 在
在![]() 轴上,过点
轴上,过点![]() 的直线交椭圆
的直线交椭圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
①若直线![]() 的斜率为
的斜率为![]() ,且
,且![]() ,求点
,求点![]() 的坐标;
的坐标;
②设直线![]() ,
,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,是否存在定点
,是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】顺次连接椭圆![]() 的四个顶点恰好构成了一个边长为
的四个顶点恰好构成了一个边长为![]() 且面积为
且面积为![]() 的菱形。
的菱形。
(1)求椭圆![]() 的方程;
的方程;
(2)![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个不同点,若直线
上的两个不同点,若直线![]() ,
,![]() 的斜率之积为
的斜率之积为![]() (以
(以![]() 为坐标原点),线段
为坐标原点),线段![]() 上有一点
上有一点![]() 满足
满足![]() ,连接并延长交椭圆
,连接并延长交椭圆![]() 于点
于点![]() ,求椭圆
,求椭圆![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现拟建一个粮仓,如图1所示,粮仓的轴截而如图2所示,ED=EC,AD![]() BC,BC⊥AB,EF⊥AB,CD交EF于点G,EF=FC=10m.
BC,BC⊥AB,EF⊥AB,CD交EF于点G,EF=FC=10m.
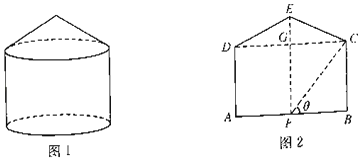
(1)设∠CFB=θ,求粮仓的体积关于θ的函数关系式;
(2)当sinθ为何值时,粮仓的体积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心在直线
的圆心在直线![]() 上,且圆
上,且圆![]() 与
与![]() :
:![]() 相切于点
相切于点![]() .过点
.过点![]() 作两条斜率之积为-2的直线分别交圆
作两条斜率之积为-2的直线分别交圆![]() 于
于![]() ,
,![]() 与
与![]() ,
,![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)设线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() ,证明:直线
,证明:直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com