
【题目】现拟建一个粮仓,如图1所示,粮仓的轴截而如图2所示,ED=EC,AD![]() BC,BC⊥AB,EF⊥AB,CD交EF于点G,EF=FC=10m.
BC,BC⊥AB,EF⊥AB,CD交EF于点G,EF=FC=10m.
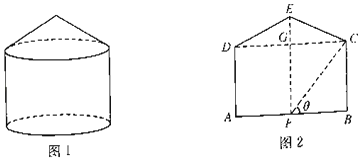
(1)设∠CFB=θ,求粮仓的体积关于θ的函数关系式;
(2)当sinθ为何值时,粮仓的体积最大?
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,平面
中,平面![]() 平面
平面![]() .四边形
.四边形![]() 为正方形,四边形
为正方形,四边形![]() 为梯形,且
为梯形,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
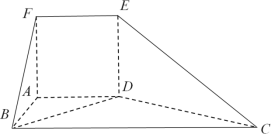
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 平面
平面![]() 若存在,求
若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现要完成下列3项抽样调查:①从20罐奶粉中抽取4罐进行食品安全卫生检查;②从某社区100户高收入家庭,270户中等收入家庭,80户低收入家庭中选出45户进行消费水平调查;③某中学报告厅有28排,每排有35个座位,一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请28名听众进行座谈.较为合理的抽样方法是( )
A.①系统抽样;②简单随机抽样;③分层抽样
B.①简单随机抽样;②分层抽样;③系统抽样
C.①分层抽样;②系统抽样;③简单随机抽样
D.①简单随机抽样;②系统抽样;③分层抽样
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线x2=4y.

(1)求抛物线在点P(2,1)处的切线方程;
(2)若不过原点的直线l与抛物线交于A,B两点(如图所示),且OA⊥OB,|OA|=![]() |OB|,求直线l的斜率.
|OB|,求直线l的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() 是底面
是底面![]() 的中心,
的中心,![]() 是线段
是线段![]() 的上一点。
的上一点。
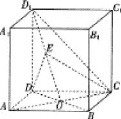
(1)若![]() 为
为![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)能否存在点![]() 使得平面
使得平面![]() 平面
平面![]() ,若能,请指出点
,若能,请指出点![]() 的位置关系,并加以证明;若不能,请说明理由。
的位置关系,并加以证明;若不能,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点![]() 在圆柱
在圆柱![]() 的底面圆
的底面圆![]() 上,
上,![]() 为圆
为圆![]() 的直径.
的直径.
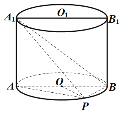
(1)若圆柱![]() 的体积
的体积![]() 为
为![]() ,
,![]() ,
,![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成的角(用反三角函数值表示结果);
所成的角(用反三角函数值表示结果);
(2)若圆柱![]() 的轴截面是边长为2的正方形,四面体
的轴截面是边长为2的正方形,四面体![]() 的外接球为球
的外接球为球![]() ,求
,求![]() 两点在球
两点在球![]() 上的球面距离.
上的球面距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() (
(![]() )的离心率是
)的离心率是![]() ,点
,点![]() 在短轴
在短轴![]() 上,且
上,且![]() 。
。
(1)球椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,过点
为坐标原点,过点![]() 的动直线与椭圆交于
的动直线与椭圆交于![]() 两点。是否存在常数
两点。是否存在常数![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com