
【题目】顺次连接椭圆![]() 的四个顶点恰好构成了一个边长为
的四个顶点恰好构成了一个边长为![]() 且面积为
且面积为![]() 的菱形。
的菱形。
(1)求椭圆![]() 的方程;
的方程;
(2)![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个不同点,若直线
上的两个不同点,若直线![]() ,
,![]() 的斜率之积为
的斜率之积为![]() (以
(以![]() 为坐标原点),线段
为坐标原点),线段![]() 上有一点
上有一点![]() 满足
满足![]() ,连接并延长交椭圆
,连接并延长交椭圆![]() 于点
于点![]() ,求椭圆
,求椭圆![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() :
:![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 、
、![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)求线段![]() 的长和
的长和![]() 的积.
的积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面立角坐标系![]() 中,过点
中,过点![]() 的圆的圆心
的圆的圆心![]() 在
在![]() 轴上,且与过原点倾斜角为
轴上,且与过原点倾斜角为![]() 的直线
的直线![]() 相切.
相切.
(1)求圆![]() 的标准方程;
的标准方程;
(2)点![]() 在直线
在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线
的切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() ,求经过
,求经过![]() 、
、![]() 、
、![]() 、
、![]() 四点的圆所过的定点的坐标.
四点的圆所过的定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现要完成下列3项抽样调查:①从20罐奶粉中抽取4罐进行食品安全卫生检查;②从某社区100户高收入家庭,270户中等收入家庭,80户低收入家庭中选出45户进行消费水平调查;③某中学报告厅有28排,每排有35个座位,一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请28名听众进行座谈.较为合理的抽样方法是( )
A.①系统抽样;②简单随机抽样;③分层抽样
B.①简单随机抽样;②分层抽样;③系统抽样
C.①分层抽样;②系统抽样;③简单随机抽样
D.①简单随机抽样;②系统抽样;③分层抽样
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x2﹣a)ex(a∈R).
(1)若函数f(x)有两个不同的极值点,求实数a的取值范围;
(2)当a=0时,若关于x的方程f(x)=m存在三个不同的实数根,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() 是底面
是底面![]() 的中心,
的中心,![]() 是线段
是线段![]() 的上一点。
的上一点。
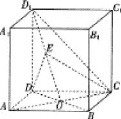
(1)若![]() 为
为![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)能否存在点![]() 使得平面
使得平面![]() 平面
平面![]() ,若能,请指出点
,若能,请指出点![]() 的位置关系,并加以证明;若不能,请说明理由。
的位置关系,并加以证明;若不能,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高考改革是教育体制改革中的重点领域和关键环节,全社会极其关注.近年来,在新高考改革中,打破文理分科的“![]() ”模式初露端倪.其中“
”模式初露端倪.其中“![]() ”指必考科目语文、数学、外语,“
”指必考科目语文、数学、外语,“![]() ”指考生根据本人兴趣特长和拟报考学校及专业的要求,从物理、化学、生物、历史、政治、地理六科中选择
”指考生根据本人兴趣特长和拟报考学校及专业的要求,从物理、化学、生物、历史、政治、地理六科中选择![]() 门作为选考科目,其中语、数、外三门课各占
门作为选考科目,其中语、数、外三门课各占![]() 分,选考科目成绩采用“赋分制”,即原始分数不直接用,而是按照学生分数在本科目考试的排名来划分等级并以此打分得到最后得分.假定
分,选考科目成绩采用“赋分制”,即原始分数不直接用,而是按照学生分数在本科目考试的排名来划分等级并以此打分得到最后得分.假定![]() 省规定:选考科目按考生成绩从高到低排列,按照占总体
省规定:选考科目按考生成绩从高到低排列,按照占总体![]() 的,以此赋分
的,以此赋分![]() 分、
分、![]() 分、
分、![]() 分、
分、![]() 分.为了让学生们体验“赋分制”计算成绩的方法,
分.为了让学生们体验“赋分制”计算成绩的方法,![]() 省某高中高一(
省某高中高一(![]() )班(共
)班(共![]() 人)举行了以此摸底考试(选考科目全考,单科全班排名,每名学生选三科计算成绩),已知这次摸底考试中的物理成绩(满分
人)举行了以此摸底考试(选考科目全考,单科全班排名,每名学生选三科计算成绩),已知这次摸底考试中的物理成绩(满分![]() 分)频率分布直方图,化学成绩(满分
分)频率分布直方图,化学成绩(满分![]() 分)茎叶图如下图所示,小明同学在这次考试中物理
分)茎叶图如下图所示,小明同学在这次考试中物理![]() 分,化学
分,化学![]() 多分.
多分.

(1)求小明物理成绩的最后得分;
(2)若小明的化学成绩最后得分为![]() 分,求小明的原始成绩的可能值;
分,求小明的原始成绩的可能值;
(3)若小明必选物理,其他两科在剩下的五科中任选,求小明此次考试选考科目包括化学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com