
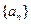 和
和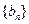 中,
中,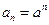 ,
,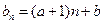 ,
,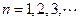 ,其中
,其中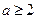 且
且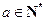 ,
,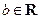 .
.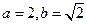 时,数列
时,数列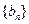 中的任意三项都不能构成等比数列;
中的任意三项都不能构成等比数列;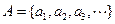 ,
,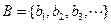 ,试问在区间
,试问在区间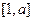 上是否存在实数
上是否存在实数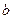 使得
使得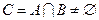 .若存在,求出
.若存在,求出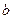 的一切可能的取值及相应的集合
的一切可能的取值及相应的集合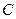 ;若不存在,试说明理由.
;若不存在,试说明理由.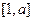 上存在实数
上存在实数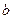 ,使
,使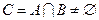 成立,且当
成立,且当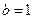 时,
时,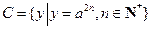 ;当
;当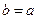 时,
时,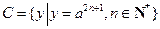 .
.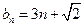 ,假设
,假设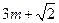 ,
,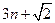 ,
,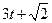 成等比数列,其中
成等比数列,其中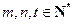 ,且彼此不等,则
,且彼此不等,则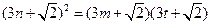 , ………2分
, ………2分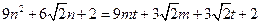 ,所以
,所以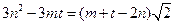 ,
,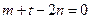 ,则
,则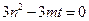 ,可得
,可得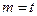 ,与
,与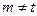 矛盾; ………4分
矛盾; ………4分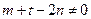 ,则
,则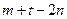 为非零整数,
为非零整数,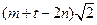 为无理数,
为无理数, 为无理数,与
为无理数,与 是整数矛盾.
是整数矛盾. 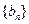 中的任意三项都不能构成等比数列. …………………6分
中的任意三项都不能构成等比数列. …………………6分 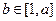 ,使
,使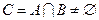 ,设
,设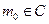 ,则
,则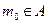 ,且
,且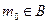 ,
,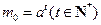 ,
,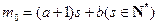 ,则
,则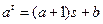 ,所以
,所以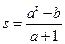 ,
,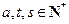 ,且
,且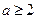 ,所以
,所以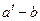 能被
能被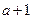 整除. …………………7分
整除. …………………7分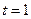 时,因为
时,因为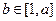 ,
, 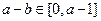 ,所以
,所以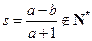 ;……9分
;……9分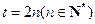 时,
时, ,
,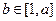 ,所以
,所以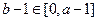 ,
,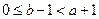 ,所以,当且仅当
,所以,当且仅当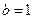 时,
时,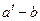 能被
能被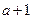 整除.…………12分
整除.…………12分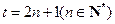 时,
时,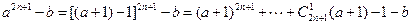 ,
,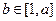 ,所以
,所以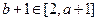 ,
,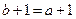 ,即
,即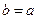 时,
时,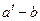 能被
能被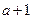 整除. ……11分
整除. ……11分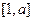 上存在实数
上存在实数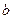 ,使
,使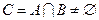 成立,且当
成立,且当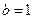 时,
时,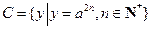 ;当
;当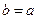 时,
时,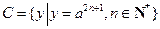 . …………12分
. …………12分

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
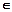
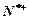 )且a3+
)且a3+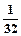 是a2,a4的等差中项,数列{bn}的前n项和Sn=n2
是a2,a4的等差中项,数列{bn}的前n项和Sn=n2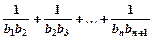 ,求证:Tn<
,求证:Tn<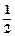
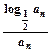 ,T/n=c1+c2+…+cn,求使T/n+n
,T/n=c1+c2+…+cn,求使T/n+n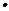 2n+1>125成立的正整数n的最小值
2n+1>125成立的正整数n的最小值查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
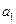 =2,且2,an,Sn成等差数列。
=2,且2,an,Sn成等差数列。
|
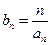 ,求数列{
,求数列{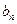 }的前n项和Tn;
}的前n项和Tn;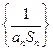 的前n项和为
的前n项和为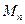 ,求证:
,求证: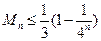 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
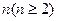 按右图方式构成三角形数表:第一行依次写上数1,2,3,……n,在下面一行的每相邻两个数的正中间上方写上这两个数之和,得到上面一行的数(比
按右图方式构成三角形数表:第一行依次写上数1,2,3,……n,在下面一行的每相邻两个数的正中间上方写上这两个数之和,得到上面一行的数(比
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
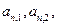 ……
……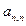 (n=1,2,3…………)分别表示第n行的第一个数,第二个数,……第n个数.则
(n=1,2,3…………)分别表示第n行的第一个数,第二个数,……第n个数.则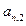 (n
(n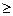 2且n
2且n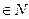 )的表达式
)的表达式A. |
B.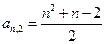 |
C.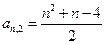 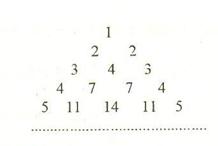 |
D.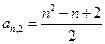 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com