
 如图所示,三棱锥A-BCD的三条侧棱AB,AC,AD两两互相垂直,O为点A在底面BCD上的射影.
如图所示,三棱锥A-BCD的三条侧棱AB,AC,AD两两互相垂直,O为点A在底面BCD上的射影.分析 (1)连接BO、DO,可以先证明出AB与平面ACD垂直,然后得到CD与AB垂直,再结合CD与AO垂直得到CD垂直于平面ABO,从而BO垂直于CD,同样的我们可以证出DO垂直于BC,从而得出点O是三角形BDC的垂心.
(2)由勾股定理是平面二维的线与线之间的关系,类比到三维空间可猜测:S△BCD2=S△ABC2+S△ACD2+S△ADB2,作AE⊥CD连BE,则BE⊥CD,S△BCD2 =$\frac{1}{4}$CD2•BE2 =$\frac{1}{4}$CD2(AB2+AE2)=$\frac{1}{4}$(AC2+AD2)(AB2+AE2),再化简即得结论.
解答 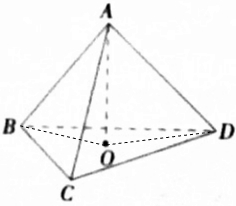 (1)证明:如图,连接BO、DO
(1)证明:如图,连接BO、DO
∵BA⊥CA,BA⊥DA,CA∩DA=A
∴BA⊥平面ACD,结合CD?平面ACD
∴CD⊥BA
又∵AO⊥平面BDC,CD?平面BDC
∴CD⊥AO
∵AO∩BA=A
∴CD⊥平面ABO,得到BO⊥CD
∴BO为DC边上的高
同理可得DO为BC边上的高
因此O为三角形BDC的垂心;
(2)解:猜测:S△BCD2=S△ABC2+S△ACD2+S△ADB2.
理由如下: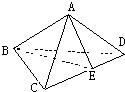
直角空间四面体ABCD中,如图作AE⊥CD连BE,
由AB,AC,AD两两垂直,可得A在底面的射影为底面△BCD的垂心,则BE⊥CD.
S△BCD2 =$\frac{1}{4}$CD2•BE2 =$\frac{1}{4}$CD2(AB2+AE2)
=$\frac{1}{4}$(AC2+AD2)(AB2+AE2)
=$\frac{1}{4}$(AC2AB2 +AD2AB2 +AC2AE2+AD2AE2 )
=$\frac{1}{4}$(AC2AB2 +AD2AB2+CD2AE2 )
=S△ABC2+S△ACD2+S△ADB2.
点评 本题考查了三垂线定理及其逆定理在多面体中的应用,属于中档题.本题考查了三垂线定理及其逆定理在多面体中的应用,属于中档题.考查类比推理,体现了数形结合的数学思想.其中由二维到三维的类比推理要注意点的性质往往推广为线的性质,线的性质往往推广为面的性质.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
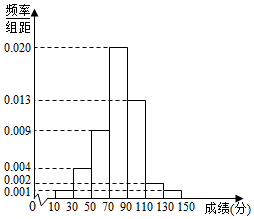 襄阳市某优质高中为了选拔学生参加“全国中学生英语能力竞赛(NEPCS)”,先在本校进行初赛(满分150分),若该校有100名学生参加初赛,并根据初赛成绩得到如图所示的频率分布直方图.
襄阳市某优质高中为了选拔学生参加“全国中学生英语能力竞赛(NEPCS)”,先在本校进行初赛(满分150分),若该校有100名学生参加初赛,并根据初赛成绩得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
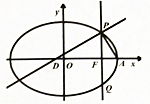 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{2}=1(a>0)$,点A,F分别为其右顶点和右焦点,过F作AF的垂线交椭圆C于P,Q两点,过P作AP的垂线交x轴于点D,若|DF|=$\frac{a+\sqrt{{a}^{2}-2}}{2}$,则椭圆C的长轴长为( )
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{2}=1(a>0)$,点A,F分别为其右顶点和右焦点,过F作AF的垂线交椭圆C于P,Q两点,过P作AP的垂线交x轴于点D,若|DF|=$\frac{a+\sqrt{{a}^{2}-2}}{2}$,则椭圆C的长轴长为( )| A. | 2 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com