
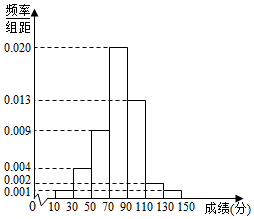
 襄阳市某优质高中为了选拔学生参加“全国中学生英语能力竞赛(NEPCS)”,先在本校进行初赛(满分150分),若该校有100名学生参加初赛,并根据初赛成绩得到如图所示的频率分布直方图.
襄阳市某优质高中为了选拔学生参加“全国中学生英语能力竞赛(NEPCS)”,先在本校进行初赛(满分150分),若该校有100名学生参加初赛,并根据初赛成绩得到如图所示的频率分布直方图.分析 (1)根据频率分布直方图,求出每个矩形的面积,即每组的概率,每组的中值乘以每组的频率之和即这100名学生参加选拔测试的平均成绩;
(2)利用频率分布直方图计算分数在[110,130)和[130,150)的人数分别予以编号,列举出随机抽出2人的所有可能,找出符合题意得情况,利用古典概型计算即可.
解答 (1)设初赛成绩的中位数为x,则:(0.001+0.004+0.009)×20+0.02×(x-70)=0.5…(4分)
解得x=81,所以初赛成绩的中位数为81;…(6分)
(2)该校学生的初赛分数在[110,130)有4人,分别记为A,B,C,D,分数在[130,150)有2人,分别记为a,b,在则6人中随机选取2人,总的事件有(A,B),(A,C),(A,D),
(A,a),(A,b),(B,C),(B,D),(B,a),(B,b),(C,D),(C,a),(C,b),(D,a),(D,b),(a,b)共15个基本事件,其中符合题设条件的基本事件有8个…(10分)
故选取的这两人的初赛成绩在频率分布直方图中处于不同组的概率为P=$\frac{8}{15}$…(12分)
点评 本题考查频率分布直方图的应用,古典概概率的计算,属于基础题.


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,三棱锥A-BCD的三条侧棱AB,AC,AD两两互相垂直,O为点A在底面BCD上的射影.
如图所示,三棱锥A-BCD的三条侧棱AB,AC,AD两两互相垂直,O为点A在底面BCD上的射影.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com