练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．若f（x）=$\sqrt{x+2}$，则f（x）的定义域是{x|x≥-2}．

    分析 根据二次根式的性质求出函数的定义域即可．

    解答 解：由题意得：x+2≥0，解得：x≥-2，
    故函数f（x）的定义域是{x|x≥-2}，
    故答案为：{x|x≥-2}．

    点评 本题考查了求函数的定义域问题，考查二次根式的性质，是一道基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    16．已知i是虚数单位，复数z=$\frac{a-i}{1-i}$（a∈R），若|z|=${∫}_{0}^{π}$（sinx-$\frac{1}{π}$）dx，则a=（　　）
    A．±1B．1C．-1D．±$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知α是第一象限角，则tanα+cotα有最小值为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．（x-$\frac{1}{x}$）n的展开式中只有第6项的二项式系数最大，则n的值为10．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

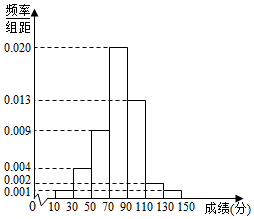    6．襄阳市某优质高中为了选拔学生参加“全国中学生英语能力竞赛（NEPCS）”，先在本校进行初赛（满分150分），若该校有100名学生参加初赛，并根据初赛成绩得到如图所示的频率分布直方图．
    （1）根据频率分布直方图，计算这100名学生参加初赛成绩的中位数；
    （2）该校推荐初赛成绩在110分以上的学生代表学校参加竞赛，为了了解情况，在该校推荐参加竞赛的学生中随机抽取2人，求选取的两人的初赛成绩在频率分布直方图中处于不同组的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

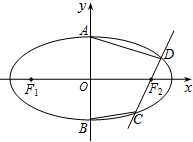    16．已知F1，F2分别是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左，右焦点，A，B分别为椭圆的上，下顶点．过椭圆的右焦点F2的直线在y轴右侧交椭圆于C，D两点．△F1CD的周长为8，且直线AC，BC的斜率之积为$-\frac{1}{4}$．
    （Ⅰ）求椭圆的方程；
    （Ⅱ）设四边形ABCD的面积为S，求S的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

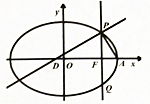    3．如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{2}=1（a＞0）$，点A，F分别为其右顶点和右焦点，过F作AF的垂线交椭圆C于P，Q两点，过P作AP的垂线交x轴于点D，若|DF|=$\frac{a+\sqrt{{a}^{2}-2}}{2}$，则椭圆C的长轴长为（　　）
    A．2B．4C．2$\sqrt{2}$D．4$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知圆O：x2+y2=r2（r＞0），点P为圆O上任意一点（不在坐标轴上），过点P作倾斜角互补的两条直线分别交圆O于另一点A，B．
    （1）当直线PA的斜率为2时，
    ①若点A的坐标为（-$\frac{1}{5}$，-$\frac{7}{5}$），求点P的坐标；
    ②若点P的横坐标为2，且PA=2PB，求r的值；
    （2）当点P在圆O上移动时，求证：直线OP与AB的斜率之积为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．我国发射的天宫一号飞行器需要建造隔热层．已知天宫一号建造的隔热层必须使用20年，每厘米厚的隔热层建造成本是6万元，天宫一号每年的能源消耗费用C（万元）与隔热层厚度x（厘米）满足关系式：C（x）=$\frac{k}{3x+8}$（0≤x≤10），若无隔热层（即x=0），则每年能源消耗费用为5万元．设f（x）为隔热层建造费用与使用20年的能源消耗费用之和．
    （1）求C（x）和f（x）的表达式；
    （2）当隔热层修建多少厘米厚时，总费用f（x）最小，并求出最小值．

    查看答案和解析>>

    同步练习册答案