
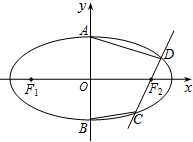
 已知F1,F2分别是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左,右焦点,A,B分别为椭圆的上,下顶点.过椭圆的右焦点F2的直线在y轴右侧交椭圆于C,D两点.△F1CD的周长为8,且直线AC,BC的斜率之积为$-\frac{1}{4}$.
已知F1,F2分别是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左,右焦点,A,B分别为椭圆的上,下顶点.过椭圆的右焦点F2的直线在y轴右侧交椭圆于C,D两点.△F1CD的周长为8,且直线AC,BC的斜率之积为$-\frac{1}{4}$.分析 (Ⅰ)设C(x1,y1),D(x2,y2),求出A(0,b),B(0,-b),4a=8,a=2,由直线AC,BC的斜率之积为$-\frac{1}{4}$.求出b,即可求解椭圆方程.
(Ⅱ)设直线$CD:x=my+\sqrt{3}$,代入$\frac{x^2}{4}+{y^2}=1$,利用韦达定理,以及弦长公式,求解三角形的面积,得到表达式,然后求解范围.
解答 解:(Ⅰ)设C(x1,y1),D(x2,y2),由题意得A(0,b),B(0,-b),4a=8,a=2(2分)
由${k_{AC}}•{k_{BC}}=\frac{{{y_1}-b}}{x_1}×\frac{{{y_1}+b}}{x_1}=\frac{{y_1^2-{b^2}}}{x_1^2}=-\frac{b^2}{a^2}=-\frac{1}{4}$,
得${b^2}=\frac{1}{4}{a^2}=1$(5分),
∴椭圆的方程为$\frac{x^2}{4}+{y^2}=1$(6分)
(Ⅱ)由(Ⅰ)知,${F_2}(\sqrt{3},0)$,故设直线$CD:x=my+\sqrt{3}$,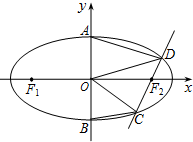
代入$\frac{x^2}{4}+{y^2}=1$得$({m^2}+4){y^2}+2\sqrt{3}my-1=0$,
则${y_1}+{y_2}=\frac{{-2\sqrt{3}m}}{{{m^2}+4}},{y_1}{y_2}=\frac{-1}{{{m^2}+4}}$(7分),
$|{{y_1}-{y_2}}|=\frac{{4\sqrt{{m^2}+1}}}{{{m^2}+4}}$,由x1>0,x2>0,得0≤m2<3,
${x_1}+{x_2}=m({y_1}+{y_2})+2\sqrt{3}=\frac{{8\sqrt{3}}}{{{m^2}+4}}$(10分)
∴面积S=S△AOD+S△BOC+S△OCD=$\frac{1}{2}$×$\frac{{8\sqrt{3}}}{{{m^2}+4}}+\frac{1}{2}×\sqrt{3}×$$\frac{{4\sqrt{{m^2}+1}}}{{{m^2}+4}}$=$\frac{{2\sqrt{3}(\sqrt{{m^2}+1}+2)}}{{{m^2}+4}}$(12分)
令$t=\sqrt{{m^2}+1}+2,t∈[3,4)$,
则$S=\frac{{2\sqrt{3}t}}{{{{(t-2)}^2}+3}}=\frac{{2\sqrt{3}}}{{t+\frac{7}{t}-4}}$在t∈[3,4)上递减
所以$S∈(\frac{{8\sqrt{3}}}{7},\frac{{3\sqrt{3}}}{2}]$.(15分)
点评 本题考查椭圆方程的求法,直线与椭圆的位置关系的综合应用,三角形的面积的求法,考查计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com