
分析 (1)①求出r2=2,直线PA的方程,代入x2+y2=2,可得5x2-4x-1=0,即可求点P的坐标;
②若点P的横坐标为2,且PA=2PB,设点P的坐标为(2,t),由垂径定理得:4(r2-d12)=16(r2-d22),因为点P(2,t)在圆O上,所以22+t2=r2,即可求r的值;
(2)当点P在圆O上移动时,求出A,B的坐标,即可证明直线OP与AB的斜率之积为定值.
解答 解:(1)①点A的坐标为(-$\frac{1}{5}$,-$\frac{7}{5}$),代入可得r2=2
直线PA的方程为y+$\frac{7}{5}$=2(x+$\frac{1}{5}$),即y=2x-1,
代入x2+y2=2,可得5x2-4x-1=0,∴点P的坐标为(1,1);
②因为直线PA与直线PB的倾斜角互补且直线PA的斜率为2,所以直线PB的斜率为-2.
设点P的坐标为(2,t),则直线PA的方程为:2x-y-4+t=0,直线PB的方程为:2x+y-t-4=0.
圆心(0,0)到直线PA,PB的距离分别为d1=$\frac{|-4+t|}{\sqrt{5}}$,d2=$\frac{|-t-4|}{\sqrt{5}}$
因为PA=2PB,所以由垂径定理得:4(r2-d12)=16(r2-d22)
所以4($\frac{|-t-4|}{\sqrt{5}}$)2-($\frac{|-4+t|}{\sqrt{5}}$)2=3r2,
又因为点P(2,t)在圆O上,所以22+t2=r2(2),联立(1)(2)解得r=$\sqrt{13}$或$\frac{\sqrt{37}}{3}$;
(2)由题意知:直线PA,PB的斜率均存在.
设点P的坐标为(x0,y0),直线OP的斜率为kOP=$\frac{{y}_{0}}{{x}_{0}}$
直线PA的斜率为k,则直线PA的方程为:y-y0=k(x-x0),
联立直线PA与圆O方程x2+y2=r2,消去y得:
(1+k2)x2+2k(y0-kx0)x+(y0-kx0)2-r2=0,
因为点P在圆O上,即x02+y02=r2,
所以(y0-kx0)2-r2=(k2-1)x02-2kx0y0,
由韦达定理得:xA=$\frac{({k}^{2}-1){x}_{0}-2k{y}_{0}}{1+{k}^{2}}$,故点A坐标为($\frac{({k}^{2}-1){x}_{0}-2k{y}_{0}}{1+{k}^{2}}$,$\frac{-2k{x}_{0}-{k}^{2}{y}_{0}+{y}_{0}}{1+{k}^{2}}$),
用“-k“代替“k“得:点B的坐标为($\frac{({k}^{2}-1){x}_{0}+2k{y}_{0}}{1+{k}^{2}}$,$\frac{2k{x}_{0}-{k}^{2}{y}_{0}+{y}_{0}}{1+{k}^{2}}$)
∴kAB=$\frac{{y}_{B}-{y}_{A}}{{x}_{B}-{x}_{A}}$=$\frac{{x}_{0}}{{y}_{0}}$
∴kABkOP=1.
综上,当点P在圆O上移动时,直线OP与AB的斜率之积为定值1
点评 本题考查直线与圆的位置关系,考查点到直线的距离公式,考查斜率的计算,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 249 | B. | 250 | C. | 251 | D. | 252 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 结论正确 | B. | 大前提错误 | C. | 小前提错误 | D. | 推理形式错误 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
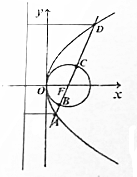 如图,抛物线:y2=4mx(m>0)和圆:x2+y2-2mx=0,直线l经过抛物线的焦点,依次交抛物线,圆于A,B,C,D四点,|AB|•|CD|=2,则m的值为( )
如图,抛物线:y2=4mx(m>0)和圆:x2+y2-2mx=0,直线l经过抛物线的焦点,依次交抛物线,圆于A,B,C,D四点,|AB|•|CD|=2,则m的值为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com